A 228-mL sample of an aqueous solution contains 2.35% MgCl₂ by mass. Exactly one-half of the magnesium ions are Mg-28, a beta emitter with a half-life of 21 hours. What is the decay rate of Mg-28 in the solution after 4.00 days? (Assume a density of 1.02 g/mL for the solution.)

Mass percent is a way to express the concentration of a solute in a solution, calculated as the mass of the solute divided by the total mass of the solution, multiplied by 100. In this case, the 2.35% MgCl2 indicates that there are 2.35 grams of MgCl2 in every 100 grams of the solution. Understanding this concept is crucial for determining the total mass of MgCl2 in the given volume of solution.

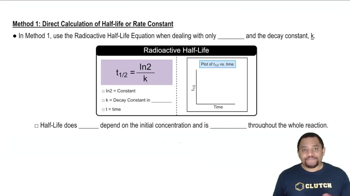
Radioactive decay is the process by which unstable atomic nuclei lose energy by emitting radiation. The half-life is the time required for half of the radioactive nuclei in a sample to decay. For Mg-28, with a half-life of 21 hours, this means that after each 21-hour period, half of the remaining Mg-28 will have decayed, which is essential for calculating the decay rate over a specified time period.

The decay rate of a radioactive substance can be calculated using the formula N(t) = N0 * (1/2)^(t/T), where N(t) is the remaining quantity after time t, N0 is the initial quantity, and T is the half-life. In this problem, after 4 days (or 96 hours), the decay of Mg-28 can be determined by applying this formula, allowing for the calculation of how much of the isotope remains in the solution.