Which of these processes are nonspontaneous? Are the nonspontaneous processes impossible? a. a bike going up a hill b. a meteor falling to Earth c. obtaining hydrogen gas from liquid water d. a ball rolling down a hill
Ch.18 - Free Energy and Thermodynamics

Chapter 18, Problem 31
Calculate the change in entropy that occurs in the system when 1.00 mole of isopropyl alcohol (C3H8O) melts at its melting point (-89.5 °C). See Table 11.9 for heats of fusion.
 Verified step by step guidance
Verified step by step guidance1
Identify the formula for calculating the change in entropy (\( \Delta S \)) during a phase change: \( \Delta S = \frac{q_{\text{rev}}}{T} \), where \( q_{\text{rev}} \) is the heat absorbed or released during the process and \( T \) is the temperature in Kelvin.
Determine the heat of fusion (\( \Delta H_{\text{fus}} \)) for isopropyl alcohol from Table 11.9. This value represents the amount of heat required to melt one mole of the substance at its melting point.
Convert the melting point from Celsius to Kelvin by adding 273.15 to the given temperature: \( T = -89.5 + 273.15 \).
Substitute the values into the entropy change formula: \( \Delta S = \frac{\Delta H_{\text{fus}}}{T} \). Ensure that \( \Delta H_{\text{fus}} \) is in joules if it is initially given in kilojoules.
Calculate \( \Delta S \) using the values obtained in the previous steps to find the change in entropy for the melting of 1.00 mole of isopropyl alcohol.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Entropy
Entropy is a measure of the disorder or randomness in a system. In thermodynamics, it quantifies the number of ways a system can be arranged, with higher entropy indicating greater disorder. When a substance changes state, such as melting, the entropy typically increases because the molecules have more freedom to move in the liquid state compared to the solid state.
Recommended video:
Guided course
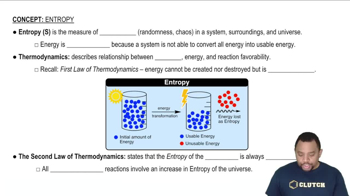
Entropy in Thermodynamics
Heats of Fusion
The heat of fusion is the amount of energy required to change a substance from solid to liquid at its melting point without changing its temperature. This value is crucial for calculating the change in entropy during phase transitions, as it provides the necessary energy input for the melting process. It is typically expressed in joules per mole (J/mol).
Recommended video:
Guided course

Heat Capacity
Gibbs Free Energy and Phase Changes
Gibbs free energy is a thermodynamic potential that helps predict the direction of chemical reactions and phase changes. At equilibrium, the change in Gibbs free energy (ΔG) is zero, and the relationship between entropy (ΔS) and enthalpy (ΔH) is given by the equation ΔG = ΔH - TΔS. Understanding this relationship is essential for calculating changes in entropy during phase transitions like melting.
Recommended video:
Guided course

Gibbs Free Energy of Reactions
Related Practice
Textbook Question
Textbook Question
Two systems, each composed of two particles represented by circles, have 20 J of total energy. Which system, A or B, has the greater entropy? Why?
Textbook Question
Two systems, each composed of three particles represented by circles, have 30 J of total energy. How many energetically equivalent ways can you distribute the particles in each system? Which system has greater entropy?
Textbook Question
Calculate the change in entropy that occurs in the system when 1.00 mole of diethyl ether (C4H10O) condenses from a gas to a liquid at its normal boiling point (34.6 °C). See Table 11.7 for heats of vaporization.
