Textbook Question
For each strong base solution, determine [OH–], [H3O+], pH, and pOH. a. 0.15 M NaOH b. 1.5×10–3 M Ca(OH)2 c. 4.8×10–4 M Sr(OH)2 d. 8.7×10–5 M KOH

 Verified step by step guidance
Verified step by step guidance

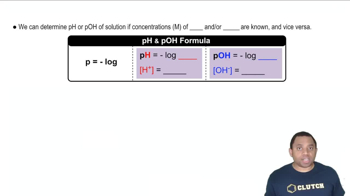

For each strong base solution, determine [OH–], [H3O+], pH, and pOH. a. 0.15 M NaOH b. 1.5×10–3 M Ca(OH)2 c. 4.8×10–4 M Sr(OH)2 d. 8.7×10–5 M KOH
For each strong base solution, determine [OH–], [H3O+], pH, and pOH. a. 8.77×10–3 M LiOH
For each strong base solution, determine [OH–], [H3O+], pH, and pOH. c. 1.9×10–4 M KOH
For each strong base solution, determine [OH–], [H3O+], pH, and pOH. d. 5.0×10–4 M Ca(OH)2
Determine the pH of a solution that is 3.85% KOH by mass. Assume that the solution has density of 1.01 g/mL.