For each strong acid solution, determine [H3O+], [OH–], and pH. b. 0.015 M HNO3
Ch.16 - Acids and Bases

Chapter 16, Problem 58
Determine the pH of each solution. a. 0.048 M HI b. 0.0895 M HClO4 c. a solution that is 0.045 M in HClO4 and 0.048 M in HCl d. a solution that is 1.09% HCl by mass (assume a density of 1.01 g/mL for the solution)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the nature of the acids involved. HI and HClO4 are strong acids, meaning they dissociate completely in water. This means the concentration of H+ ions in the solution is equal to the concentration of the acid.
Step 2: Calculate the pH for each solution using the formula: \( \text{pH} = -\log[\text{H}^+] \). For part (a), use the concentration of HI, which is 0.048 M.
Step 3: For part (b), use the concentration of HClO4, which is 0.0895 M, to find the pH using the same formula.
Step 4: For part (c), since both HClO4 and HCl are strong acids, add their concentrations to find the total [H+] and then calculate the pH.
Step 5: For part (d), convert the percentage concentration of HCl to molarity. Use the formula: \( \text{Molarity} = \frac{\text{mass percent} \times \text{density} \times 10}{\text{molar mass of HCl}} \). Then, calculate the pH using the molarity obtained.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Strong Acids and pH Calculation
Strong acids, such as HI and HClO4, completely dissociate in water, meaning that the concentration of hydrogen ions (H+) in solution is equal to the concentration of the acid. The pH of a solution is calculated using the formula pH = -log[H+]. For example, a 0.048 M HI solution will have a pH of -log(0.048), which can be computed directly.
Recommended video:
Guided course
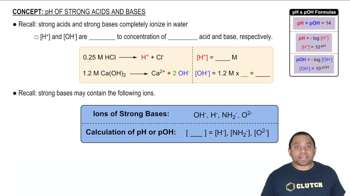
pH of Strong Acids and Bases
Mixed Acid Solutions
When dealing with mixed acid solutions, such as the one containing both HClO4 and HCl, the total concentration of H+ ions is the sum of the contributions from each acid. Since both are strong acids, their concentrations can be added directly to find the total H+ concentration, which is then used to calculate the overall pH of the solution.
Recommended video:
Guided course

Solution Components
Mass Percent Concentration to Molarity Conversion
To determine the pH of a solution given in mass percent, such as 1.09% HCl, it is necessary to convert this to molarity. This involves calculating the mass of HCl in a given volume of solution, using the density to find the volume, and then converting the mass to moles using the molar mass of HCl. The resulting molarity can then be used to find the pH.
Recommended video:
Guided course

Mass Percent Conversion
Related Practice
Textbook Question
Textbook Question
For each strong acid solution, determine [H3O+], [OH–], and pH. c. a solution that is 0.052 M in HBr and 0.020 M in HNO3
Textbook Question
For each strong acid solution, determine [H3O+], [OH–], and pH. d. a solution that is 0.655% HNO3 by mass (assume a density of 1.01 g/mL for the solution)
Textbook Question
What mass of HI must be present in 0.250 L of solution to obtain a solution with each pH value?
a. pH = 1.25 b. pH = 1.75 c. pH = 2.85
Textbook Question
What mass of HClO4 must be present in 0.500 L of solution to obtain a solution with each pH value? a. pH = 2.50 b. pH = 1.50 c. pH = 0.50
Textbook Question
What is the pH of a solution in which 224 mL of HCl(g), measured at 27.2 °C and 1.02 atm, is dissolved in 1.5 L of aqueous solution?
