For the reaction A(g) ⇌ 2 B(g), a reaction vessel initially contains only A at a pressure of PA = 1.32 atm. At equilibrium, PA = 0.25 atm. Calculate the value of Kp. (Assume no changes in volume or temperature.)

Verified step by step guidance

Identify the initial and equilibrium pressures of A. Initially, \( P_A = 1.32 \) atm and at equilibrium, \( P_A = 0.25 \) atm.

Determine the change in pressure of A, \( \Delta P_A = P_{A,\text{initial}} - P_{A,\text{equilibrium}} = 1.32 - 0.25 \) atm.

Use the stoichiometry of the reaction to find the change in pressure of B. Since \( A \) converts to \( 2B \), the change in pressure of B is \( 2 \times \Delta P_A \).

Calculate the equilibrium pressure of B, \( P_B = 2 \times \Delta P_A \).

Use the equilibrium pressures to calculate \( K_p \) using the expression \( K_p = \frac{(P_B)^2}{P_A} \).

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Equilibrium Constant (Kp)

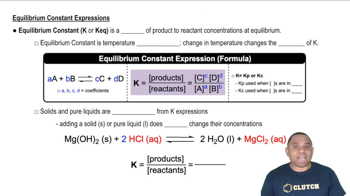
The equilibrium constant, Kp, is a ratio that expresses the relationship between the partial pressures of the products and reactants at equilibrium for a given reaction. For the reaction A(g) ⇌ 2 B(g), Kp is calculated using the formula Kp = (PB^2) / (PA), where PB and PA are the partial pressures of B and A, respectively. This constant provides insight into the extent of the reaction and whether products or reactants are favored at equilibrium.

Partial Pressure

Partial pressure is the pressure exerted by a single component of a gas mixture. In the context of the reaction A(g) ⇌ 2 B(g), the partial pressures of A and B are crucial for calculating Kp. The total pressure in a system is the sum of the partial pressures of all gases present, and understanding how these pressures change during a reaction is essential for determining equilibrium conditions.

Le Chatelier's Principle

Le Chatelier's Principle states that if a dynamic equilibrium is disturbed by changing the conditions, the system will adjust to counteract the change and restore a new equilibrium. In this reaction, if the pressure of A decreases, the system will shift to produce more B to re-establish equilibrium. This principle helps predict how changes in concentration, pressure, or temperature affect the position of equilibrium.

Recommended video:

Guided course

07:32

Le Chatelier's Principle

Related Practice

Textbook Question

Consider the following reaction: H₂(g) + I₂(g) ⇌ 2 HI(g) Complete the table. Assume that all concentrations are equilibrium concentrations in M.

T (°C) [H₂] [I₂] [HI] Kc

25 0.0355 0.0388 0.922 _

340 _ 0.0455 0.387 9.6

445 0.0485 0.0468 _ 50.2

Textbook Question

Consider the reaction: 2 NO(g) + Br₂(g) ⇌ 2 NOBr(g) K_p = 28.4 at 298K In a reaction mixture at equilibrium, the partial pressure of NO is 108 torr and that of Br₂ is 126 torr. What is the partial pressure of NOBr in this mixture?

Textbook Question

Consider the reaction: SO₂Cl₂(g) ⇌ SO₂(g) + Cl₂(g) K_p = 2.91⨉10³ at 298 K In a reaction at equilibrium, the partial pressure of SO₂ is 137 torr and that of Cl₂ is 285 torr. What is the partial pressure of SO₂Cl₂in this mixture?