The evaporation of a 120-nm film of n-pentane from a single crystal of aluminum oxide is zero order with a rate constant of 1.92⨉1013 molecules/cm2•s at 120 K. a. If the initial surface coverage is 8.9⨉1016 molecules/cm2, how long will it take for one-half of the film to evaporate?

The kinetics of this reaction were studied as a function of temperature. (The reaction is first order in each reactant and second order overall.)
C2H5Br(aq) + OH- (aq) → C2H5OH(l) + Br- (aq)
Temperature (°C) k (L,mol •s)
25 8.81⨉10-5
35 0.000285
45 0.000854
55 0.00239
65 0.00633
c. If a reaction mixture is 0.155 M in C2H5Brand 0.250 M in OH-, what is the initial rate of the reaction at 75 °C?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
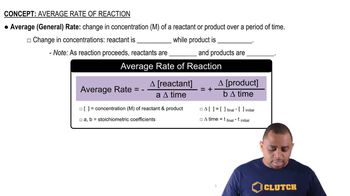
Key Concepts
Reaction Order

Rate Constant (k)

Initial Rate of Reaction
The kinetics of this reaction were studied as a function of temperature. (The reaction is first order in each reactant and second order overall.)
C2H5Br(aq) + OH- (aq) → C2H5OH(l) + Br- (aq)
Temperature (°C) k (L,mol •s)
25 8.81⨉10-5
35 0.000285
45 0.000854
55 0.00239
65 0.00633
a. Determine the activation energy and frequency factor for the reaction.
The kinetics of this reaction were studied as a function of temperature. (The reaction is first order in each reactant and second order overall.)
C2H5Br(aq) + OH- (aq) → C2H5OH(l) + Br- (aq)
Temperature (°C) k (L,mol •s)
25 8.81⨉10-5
35 0.000285
45 0.000854
55 0.00239
65 0.00633
b. Determine the rate constant at 15 °C.
The reaction 2 N2O5 → 2 N2O4 + O2 takes place at around room temperature in solvents such as CCl4. The rate constant at 293 K is found to be 2.35⨉10-4 s-1, and at 303 K the rate constant is found to be 9.15⨉10-4 s-1. Calculate the frequency factor for the reaction.
This reaction has an activation energy of zero in the gas phase: CH3 + CH3 → C2H6 a. Would you expect the rate of this reaction to change very much with temperature?
