The decomposition of XY is second order in XY and has a rate constant of 7.02⨉10-3 M-1• s-1 at a certain temperature. a. What is the half-life for this reaction at an initial concentration of 0.100 M?
Ch.14 - Chemical Kinetics

Chapter 14, Problem 57a
The half-life for the radioactive decay of U-238 is 4.5 billion years and is independent of initial concentration. How long will it take for 10% of the U-238 atoms in a sample of U-238 to decay?
 Verified step by step guidance
Verified step by step guidance1
Understand the concept of half-life, which is the time required for half of the radioactive substance to decay. For U-238, this time is 4.5 billion years.
Set up the decay formula using the exponential decay model: \( N = N_0 \times e^{-kt} \), where \( N \) is the remaining amount of substance, \( N_0 \) is the initial amount, \( k \) is the decay constant, and \( t \) is time.
Calculate the decay constant \( k \) using the half-life formula: \( k = \frac{\ln(2)}{T_{1/2}} \), where \( T_{1/2} \) is the half-life of the substance.
Determine the time \( t \) when 90% of the original U-238 remains (since 10% has decayed). Use the decay formula, substituting \( N = 0.9N_0 \) and solve for \( t \).
Plug in the value of \( k \) from step 3 into the equation from step 4 and solve for \( t \) to find out how long it takes for 10% of the U-238 to decay.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Half-life
Half-life is the time required for half of the radioactive nuclei in a sample to decay. It is a constant property of each radioactive isotope, meaning it does not change regardless of the amount of substance present. For U-238, the half-life is 4.5 billion years, indicating that after this period, half of the original amount will have transformed into other elements.
Recommended video:
Guided course

Zero-Order Half-life
Exponential Decay
Radioactive decay follows an exponential decay model, where the quantity of a substance decreases at a rate proportional to its current value. This means that the decay process is continuous and can be described mathematically using the decay constant, which is related to the half-life. Understanding this concept is crucial for calculating the remaining quantity of a substance after a certain period.
Recommended video:
Guided course
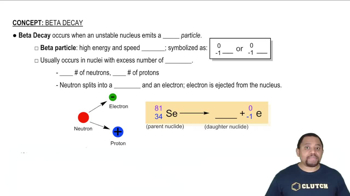
Beta Decay
Decay Calculation
To determine how long it takes for a specific percentage of a radioactive substance to decay, one can use the formula derived from the exponential decay model. For U-238, to find the time for 10% decay, one can set up the equation based on the initial amount and the remaining amount after decay, applying logarithmic functions to solve for time. This calculation illustrates the relationship between time, decay percentage, and half-life.
Recommended video:
Guided course

Beta Decay
Related Practice
Textbook Question
Textbook Question
The half-life for the radioactive decay of U-238 is 4.5 billion years and is independent of initial concentration. If a sample of U-238 initially contained 1.5⨉1018 atoms when the universe was formed 13.8 billion years ago, how many U-238 atoms does it contain today?
Textbook Question
The half-life for the radioactive decay of C-14 is 5730 years and is independent of the initial concentration. How long does it take for 25% of the C-14 atoms in a sample of C-14 to decay?
Textbook Question
The half-life for the radioactive decay of C-14 is 5730 years and is independent of the initial concentration. If a sample of C-14 initially contains 1.5 mmol of C-14, how many millimoles are left after 2255 years?
