Textbook Question
The tabulated data were collected for this reaction at a certain temperature: X2Y → 2 X + Y a. Determine the order of the reaction and the value of the rate constant at this temperature.

 Verified step by step guidance
Verified step by step guidance


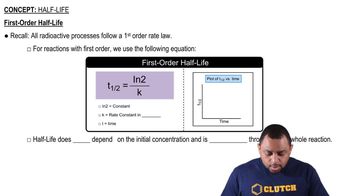
The tabulated data were collected for this reaction at a certain temperature: X2Y → 2 X + Y a. Determine the order of the reaction and the value of the rate constant at this temperature.
The tabulated data were collected for this reaction at a certain temperature: X2Y → 2 X + Y c. What is the concentration of X after 10.0 hours?
Dinitrogen pentoxide decomposes in the gas phase to form nitrogen dioxide and oxygen gas. The reaction is first order in dinitrogen pentoxide and has a half-life of 2.81 h at 25 °C. If a 1.5-L reaction vessel initially contains 745 torr of N2O5 at 25 °C, what partial pressure of O2 is present in the vessel after 215 minutes?