Skip to main content
Pearson+ LogoPearson+ Logo
Ch.13 - Solutions
All textbooksTro 4th EditionCh.13 - SolutionsProblem 75
Chapter 13, Problem 75

A solution contains 4.08 g of chloroform (CHCl3) and 9.29 g of acetone (CH3COCH3). The vapor pressures at 35 °C of pure chloroform and pure acetone are 295 torr and 332 torr, respectively. Assuming ideal behavior, calculate the vapor pressures of each of the components and the total vapor pressure above the solution. The experimentally measured total vapor pressure of the solution at 35 °C is 312 torr. Is the solution ideal? If not, what can you say about the relative strength of chloroform–acetone interactions compared to the acetone–acetone and chloroform–chloroform interactions?

Verified step by step guidance
1
Calculate the mole fraction of chloroform (CHCl_3) in the solution. Use the formula: \( \text{mole fraction of CHCl}_3 = \frac{\text{moles of CHCl}_3}{\text{moles of CHCl}_3 + \text{moles of CH}_3\text{COCH}_3} \).
Calculate the mole fraction of acetone (CH_3COCH_3) in the solution. Use the formula: \( \text{mole fraction of CH}_3\text{COCH}_3 = \frac{\text{moles of CH}_3\text{COCH}_3}{\text{moles of CHCl}_3 + \text{moles of CH}_3\text{COCH}_3} \).
Use Raoult's Law to calculate the partial vapor pressure of chloroform: \( P_{\text{CHCl}_3} = \text{mole fraction of CHCl}_3 \times P^0_{\text{CHCl}_3} \), where \( P^0_{\text{CHCl}_3} \) is the vapor pressure of pure chloroform.
Use Raoult's Law to calculate the partial vapor pressure of acetone: \( P_{\text{CH}_3\text{COCH}_3} = \text{mole fraction of CH}_3\text{COCH}_3 \times P^0_{\text{CH}_3\text{COCH}_3} \), where \( P^0_{\text{CH}_3\text{COCH}_3} \) is the vapor pressure of pure acetone.
Calculate the total vapor pressure of the solution by adding the partial pressures: \( P_{\text{total}} = P_{\text{CHCl}_3} + P_{\text{CH}_3\text{COCH}_3} \). Compare this with the experimentally measured total vapor pressure to determine if the solution is ideal. If the calculated pressure is different from the experimental value, discuss the relative strength of interactions.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Raoult's Law

Raoult's Law states that the vapor pressure of a solvent in a solution is directly proportional to the mole fraction of the solvent in the solution. For a solution containing multiple components, the total vapor pressure can be calculated by summing the partial pressures of each component, which are determined by their respective mole fractions and pure component vapor pressures.
Recommended video:
Guided course
02:40
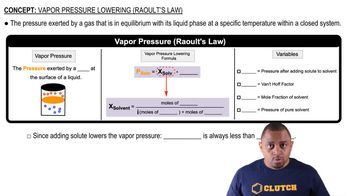
Raoult's Law and Vapor Pressure

Mole Fraction

The mole fraction is a way of expressing the concentration of a component in a mixture. It is calculated by dividing the number of moles of a specific component by the total number of moles of all components in the solution. This concept is crucial for applying Raoult's Law, as it helps determine the contribution of each component to the overall vapor pressure.
Recommended video:
Guided course
00:36
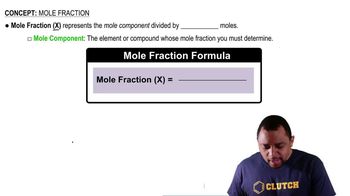
Mole Fraction Formula

Ideal vs. Non-Ideal Solutions

An ideal solution is one where the interactions between different molecules are similar to those between like molecules, leading to predictable behavior according to Raoult's Law. If the measured vapor pressure deviates from the expected values, it indicates non-ideal behavior, suggesting that the interactions between different components (e.g., chloroform and acetone) are stronger or weaker than those between the same type of molecules, affecting the overall vapor pressure.
Recommended video:
Guided course
01:15
Ideal Gas Law Formula
Related Practice
Textbook Question

A solution contains 50.0 g of heptane (C7H16) and 50.0 g of octane (C8H18) at 25 °C. The vapor pressures of pure heptane and pure octane at 25 °C are 45.8 torr and 10.9 torr, respectively. Assuming ideal behavior, answer the following: d. Why is the composition of the vapor different from the composition of the solution?

Textbook Question

A solution contains a mixture of pentane and hexane at room temperature. The solution has a vapor pressure of 258 torr. Pure pentane and hexane have vapor pressures of 425 torr and 151 torr, respectively, at room temperature. What is the mole fraction composition of the mixture? (Assume ideal behavior.)

Textbook Question

A glucose solution contains 55.8 g of glucose (C6H12O6) in 455 g of water. Determine the freezing point and boiling point of the solution.