A minimum energy of 7.21⨉10^-19 J is required to produce the photoelectric effect in chromium metal. (b) Light with a wavelength of 2.50⨉10^-7 m falls on a piece of chromium in an evacuated glass tube. What is the minimum de Broglie wavelength of the emitted electrons? (Note that the energy of the incident light must be conserved; that is, the photon's energy must equal the sum of the energy needed to eject the electron plus the kinetic energy of the electron.)

Verified step by step guidance

Calculate the energy of the incident photon using the formula: \( E = \frac{hc}{\lambda} \), where \( h \) is Planck's constant (6.626 \times 10^{-34} \text{ J s}), \( c \) is the speed of light (3.00 \times 10^8 \text{ m/s}), and \( \lambda \) is the wavelength of the light (2.50 \times 10^{-7} \text{ m}).

Determine the kinetic energy of the emitted electron by subtracting the minimum energy required to eject the electron (7.21 \times 10^{-19} \text{ J}) from the energy of the incident photon calculated in the previous step.

Use the kinetic energy of the electron to find its velocity using the formula: \( KE = \frac{1}{2}mv^2 \), where \( m \) is the mass of an electron (9.11 \times 10^{-31} \text{ kg}). Solve for \( v \).

Calculate the de Broglie wavelength of the emitted electron using the formula: \( \lambda = \frac{h}{mv} \), where \( h \) is Planck's constant and \( v \) is the velocity of the electron found in the previous step.

Ensure all units are consistent and check calculations for any errors.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Photoelectric Effect

The photoelectric effect refers to the phenomenon where electrons are emitted from a material when it absorbs light of sufficient energy. The energy of the incoming photons must exceed a certain threshold, known as the work function, for electrons to be ejected. This effect demonstrates the particle nature of light, as photons carry quantized energy proportional to their frequency, described by the equation E = hf, where E is energy, h is Planck's constant, and f is frequency.

Photon Energy and Wavelength

The energy of a photon is inversely related to its wavelength, described by the equation E = hc/λ, where E is energy, h is Planck's constant, c is the speed of light, and λ is the wavelength. In the context of the photoelectric effect, the energy of the incident light must be calculated to determine if it can overcome the work function of the material. If the photon energy exceeds the work function, the excess energy contributes to the kinetic energy of the emitted electrons.

de Broglie Wavelength

The de Broglie wavelength is a concept that describes the wave-like behavior of particles, such as electrons. It is given by the equation λ = h/p, where λ is the wavelength, h is Planck's constant, and p is the momentum of the particle. For emitted electrons, their momentum can be derived from their kinetic energy, allowing us to calculate their de Broglie wavelength after they are ejected from the chromium metal.

Recommended video:

Guided course

00:58

De Broglie Wavelength Formula

Related Practice

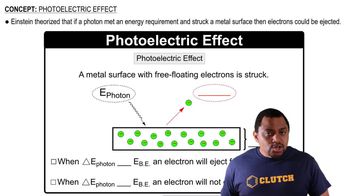
Textbook Question

In the Bohr model of atomic structure, electrons are constrained to orbit a nucleus at specific distances, given by the equation

where r is the radius of the orbit, Z is the charge on the nucleus, a0 is the Bohr radius and has a value of 5.292 * 10-11 m, and n is a positive integer (n = 1, 2, 3...) like a principal quantum number. Furthermore, Bohr concluded that the energy level E of an electron in a given orbit is

where e is the charge on an electron. Derive an equation that will let you calculate the difference ∆E between any two energy levels. What relation does your equation have to the Balmer–Rydberg equation?

Textbook Question

Assume that the rules for quantum numbers are different and that the spin quantum number ms can have any of three values, ms = -1/2, 0, +1/2, while all other rules remain the same.(a) Draw an orbital-filling diagram for the element with Z = 25, showing the individual electrons in the outer-most subshell as up arrows, down arrows, or 0. How many partially filled orbitals does the element have?

Textbook Question

A minimum energy of 7.21⨉10^-19 J is required to produce the photoelectric effect in chromium metal. (a) What is the minimum frequency of light needed to remove an electron from chromium?

Textbook Question

An energetically excited hydrogen atom has its electron in a 5f subshell. The electron drops down to the 3d subshell, releasing a photon in the process. (b) What wavelength of light is emitted by the process?

Textbook Question

An energetically excited hydrogen atom has its electron in a 5f subshell. The electron drops down to the 3d subshell, releasing a photon in the process. (c) The hydrogen atom now has a single electron in the 3d subshell. What is the energy in kJ/mol required to remove this electron?