Skip to main content
Pearson+ LogoPearson+ Logo
Ch.21 - Transition Elements and Coordination Chemistry
All textbooksMcMurry 8th EditionCh.21 - Transition Elements and Coordination ChemistryProblem 134
Chapter 21, Problem 134

Spinach contains a lot of iron but is not a good source of dietary iron because nearly all the iron is tied up in the oxalate complex 3Fe(C2O4)3^3-. (a) The formation constant Kf for 3Fe(C2O4)3^3- is 3.3 * 10^20. Calculate the equilibrium concentration of free Fe^3+ in a 0.100 M solution of 3Fe(C2O4)3^3-. (Ignore any acid–base reactions.)

Verified step by step guidance
1
Identify the relevant chemical equilibrium: The complex ion formation can be represented by the equation: \[ \text{Fe}^{3+} + 3\text{C}_2\text{O}_4^{2-} \rightleftharpoons \text{Fe(C}_2\text{O}_4\text{)}_3^{3-} \]
Write the expression for the formation constant \( K_f \): \[ K_f = \frac{[\text{Fe(C}_2\text{O}_4\text{)}_3^{3-}]}{[\text{Fe}^{3+}][\text{C}_2\text{O}_4^{2-}]^3} \]
Assume that the initial concentration of \( \text{Fe(C}_2\text{O}_4\text{)}_3^{3-} \) is 0.100 M and that it dissociates slightly to form \( \text{Fe}^{3+} \) and \( \text{C}_2\text{O}_4^{2-} \). Let \( x \) be the concentration of \( \text{Fe}^{3+} \) at equilibrium.
Express the equilibrium concentrations in terms of \( x \): \([\text{Fe}^{3+}] = x\), \([\text{C}_2\text{O}_4^{2-}] = 3x\), and \([\text{Fe(C}_2\text{O}_4\text{)}_3^{3-}] = 0.100 - x\).
Substitute these expressions into the \( K_f \) expression and solve for \( x \): \[ 3.3 \times 10^{20} = \frac{0.100 - x}{x(3x)^3} \]

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Formation Constant (Kf)

The formation constant, Kf, quantifies the stability of a complex ion in solution. It is defined as the equilibrium constant for the formation of a complex from its constituent ions. A high Kf value, such as 3.3 * 10^20 for 3Fe(C2O4)3^3-, indicates that the complex is very stable and that the concentration of free ions in solution will be very low.
Recommended video:
Guided course
02:20
Complex Ions and Formation Constant

Equilibrium Concentration

Equilibrium concentration refers to the concentrations of reactants and products in a chemical reaction at equilibrium. In this context, it is crucial to determine the concentration of free Fe^3+ ions when the complex 3Fe(C2O4)3^3- is present. The relationship between the formation constant and the equilibrium concentrations allows us to calculate the amount of free Fe^3+ in the solution.
Recommended video:
Guided course
02:35
Thermal Equilibrium

Complex Ion Chemistry

Complex ion chemistry involves the study of ions that consist of a central metal ion bonded to surrounding molecules or anions, known as ligands. In this case, Fe^3+ is the central metal ion, and oxalate (C2O4^2-) acts as a ligand. Understanding how these complexes form and dissociate is essential for predicting the behavior of metal ions in solution, particularly in terms of their availability for biological processes.
Recommended video:
Guided course
02:09
Complex Ion Formation
Related Practice
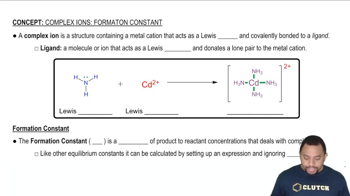
Textbook Question

There are three coordination compounds with the empirical

formula Co1NH3231NO223 in which all the nitrite ions

are bonded through the N atom. Two isomers have the

same molar mass but different nonzero dipole moments.

The third compound is a salt with singly charged ions and a molar mass twice that of the other compounds.

(a) Draw the structures of the isomeric compounds.