In acidic aqueous solution, the complex trans-[Co(en)2Cl2]+ under...

Question

In acidic aqueous solution, the complex trans-[Co(en)2Cl2]+ undergoes the following substitution reaction: <REACTION> The reaction is first order in trans-[Co(en)2Cl2]+, and the rate constant at 25 °C is 3.2 × 10⁻⁵ s⁻¹. (a) What is the half-life of the reaction in hours? (b) If the initial concentration of trans-[Co(en)2Cl2]+ is 0.138 M, what is its molarity after a reaction time of 16.5 h? (c) Devise a possible reaction mechanism with a unimolecular rate-determining step.

Accepted Answer

Step 1: To find the half-life of a first-order reaction, use the formula: $t_{1/2} = \frac{0.693}{k}$, where $k$ is the rate constant.. Step 2: Convert the rate constant from seconds to hours by multiplying by the number of seconds in an hour (3600 s/h).. Step 3: For part (b), use the first-order integrated rate law: $[A] = [A]_0 e^{-kt}$, where $[A]_0$ is the initial concentration, $k$ is the rate constant, and $t$ is the time in hours.. Step 4: Substitute the given values into the integrated rate law to find the concentration after 16.5 hours.. Step 5: For part (c), propose a reaction mechanism. A possible mechanism could involve the dissociation of one ligand from the complex to form an intermediate, followed by the substitution of another ligand. The rate-determining step would be the slowest step, likely the initial dissociation.

Key Concepts

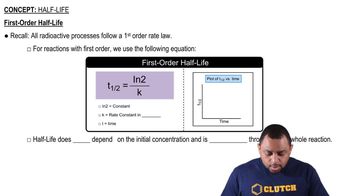
First-Order Reactions

Half-Life Calculation

Reaction Mechanism