Thorium-232 decays by a 10-step series of nuclear reactions, ultimately yielding lead-208, along with 6 α particles and 4 β particles. How much energy (in kJ/mol) is released during the overall process? The relevant masses are 232Th = 232.038 054, 208Pb = 207.976 627, electron = 0.000 548 6, and 4He = 4.002 603.

Verified step by step guidance

Step 1: Identify the nuclear reaction process. Thorium-232 decays to lead-208 through a series of nuclear reactions, emitting 6 alpha particles and 4 beta particles.

Step 2: Calculate the total mass of the reactants. The initial mass is the mass of Thorium-232, which is 232.038 054 u.

Step 3: Calculate the total mass of the products. This includes the mass of lead-208, 6 alpha particles, and 4 beta particles. Use the given masses: 208Pb = 207.976 627 u, 4He = 4.002 603 u, and electron = 0.000 548 6 u.

Step 4: Determine the mass defect. Subtract the total mass of the products from the total mass of the reactants to find the mass defect, which represents the mass converted to energy.

Step 5: Use Einstein's equation, E=mc^2, to calculate the energy released. Convert the mass defect from atomic mass units to kilograms, and then calculate the energy in joules. Finally, convert the energy to kJ/mol by considering Avogadro's number.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Nuclear Decay

Nuclear decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. This can occur through various types of decay, including alpha (α) decay, where helium nuclei are emitted, and beta (β) decay, where electrons or positrons are emitted. Understanding the types of decay is crucial for analyzing the transformation of thorium-232 into lead-208 and the associated particle emissions.

Mass-Energy Equivalence

Mass-energy equivalence, expressed by Einstein's equation E=mc², states that mass can be converted into energy and vice versa. In nuclear reactions, the mass of the products is often less than the mass of the reactants, and this mass difference is converted into energy. Calculating the energy released during the decay of thorium-232 involves determining the mass defect and applying this principle to find the energy in kJ/mol.

Molar Mass and Energy Calculations

Molar mass is the mass of one mole of a substance, typically expressed in grams per mole. To calculate the energy released in kJ/mol during the decay process, one must first determine the total mass of the reactants and products, find the mass defect, and then convert this mass defect into energy using the mass-energy equivalence principle. This involves converting the energy from joules to kilojoules and adjusting for the number of moles involved in the reaction.

Recommended video:

Guided course

03:12

Molar Mass Calculation Example

Related Practice

Textbook Question

Calculate the binding energy (in MeV/nucleon) for the following nuclei. (a)58Ni (atomic mass = 57.93535)

Textbook Question

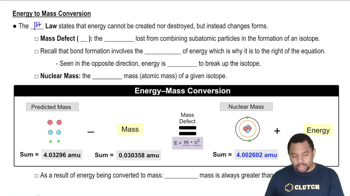
Calculate the binding energy (in MeV/nucleon) for the following nuclei. (b) 84Kr (atomic mass = 83.91151)

Textbook Question

What is the energy change ∆E (in kJ/mol) when an a particle is emitted from 174Ir? The atomic mass of 174Ir is 173.96666 the atomic mass of 170Re is 169.95804, and the atomic mass of a 4He atom is 4.00260.

Textbook Question

The radioactive isotope 100Tc decays to form the stable iso-tope 100Mo. (a) There are two possible pathways for this decay. Write balanced equations for both.

Textbook Question

The radioactive isotope 100Tc decays to form the stable iso-tope 100Mo. (b) Only one of the pathways is observed. Calculate the energy released by both pathways, and explain why only one is observed. Relevant masses are: 100Tc = 99.907 657, 100Mo = 99.907 48, electron = 0.000 548 6.