A particular saturated solution of Ca3(PO4)2 has [Ca2+] = [PO43-] = 2.9 x 10^-7 M. (c) What is [PO43-] in a saturated solution that has [Ca2+] = 0.010 M?

Verified step by step guidance

Identify the solubility product expression for calcium phosphate, \( \text{Ca}_3(\text{PO}_4)_2 \). The dissolution can be represented as: \( \text{Ca}_3(\text{PO}_4)_2 (s) \rightleftharpoons 3\text{Ca}^{2+} (aq) + 2\text{PO}_4^{3-} (aq) \).

Write the expression for the solubility product constant, \( K_{sp} \), which is given by: \( K_{sp} = [\text{Ca}^{2+}]^3 [\text{PO}_4^{3-}]^2 \).

Use the initial condition where \([\text{Ca}^{2+}] = [\text{PO}_4^{3-}] = 2.9 \times 10^{-7} \text{ M}\) to calculate \( K_{sp} \). Substitute these values into the \( K_{sp} \) expression to find its value.

Now, consider the new condition where \([\text{Ca}^{2+}] = 0.010 \text{ M}\). Substitute this value into the \( K_{sp} \) expression: \( K_{sp} = (0.010)^3 [\text{PO}_4^{3-}]^2 \).

Solve for \([\text{PO}_4^{3-}]\) by rearranging the equation: \([\text{PO}_4^{3-}] = \sqrt{\frac{K_{sp}}{(0.010)^3}}\).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Saturation and Solubility Product (Ksp)

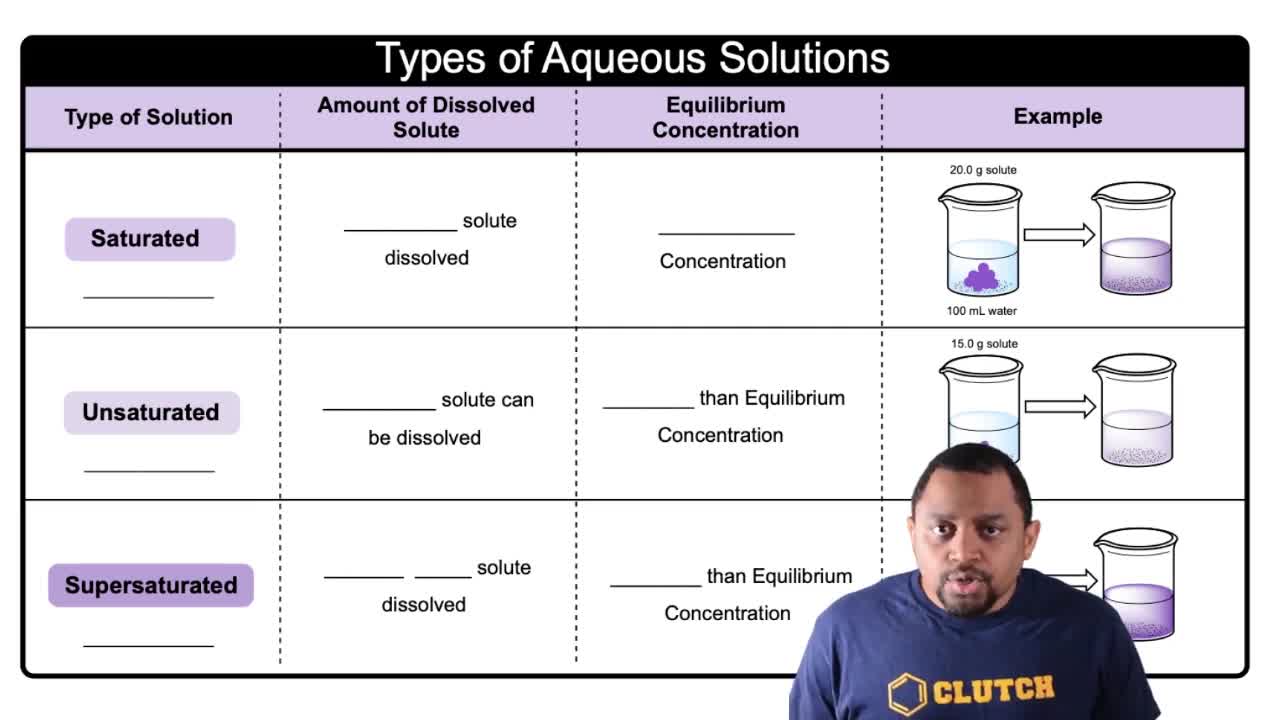
Saturation refers to the point at which a solution can no longer dissolve additional solute at a given temperature. The solubility product constant (Ksp) is an equilibrium constant that quantifies the solubility of a sparingly soluble ionic compound. For calcium phosphate, Ca3(PO4)2, Ksp is determined by the concentrations of its ions in a saturated solution, specifically [Ca2+] and [PO43-].

Stoichiometry of Dissociation

The stoichiometry of dissociation describes how a compound breaks down into its constituent ions in solution. For Ca3(PO4)2, the dissociation can be represented as Ca3(PO4)2 ⇌ 3Ca2+ + 2PO43-. This means that for every mole of Ca3(PO4)2 that dissolves, three moles of Ca2+ and two moles of PO43- are produced, establishing a relationship between their concentrations in a saturated solution.

Concentration Relationships in Saturated Solutions

In a saturated solution, the concentrations of the ions are related through the Ksp expression. For Ca3(PO4)2, Ksp = [Ca2+]^3[PO43-]^2. When the concentration of one ion changes, the concentration of the other must adjust to maintain the equilibrium defined by Ksp. This relationship allows us to calculate the concentration of PO43- when [Ca2+] is known.

Recommended video:

Guided course

03:20

Different Types of Aqueous Solutions

Related Practice

Textbook Question

The titration of 0.02500 L of a diprotic acid solution with 0.1000 M NaOH requires 34.72 mL of titrant to reach the second equivalence point. The pH is 3.95 at the first equiva-lence point and 9.27 at the second equivalence point. If the acid solution contained 0.2015 g of the acid, what is the molar mass, pKa1, and pKa2 of the acid?

Textbook Question

For each of the following compounds, write a balanced net ionic equation for the dissolution of the compound in water, and write the equilibrium-constant expression for Ksp. (d) Hg2Cl2

Textbook Question

Use the following solubility data to calculate a value of K_sp for each compound. (a) SrF₂: 1.03 x 10^-3 M (b) CuI: 1.05 x 10^-6 M