A 100.0 mL sample of a solution that is 0.100 M in HCl and 0.100 M in HCN is titrated with 0.100 M NaOH. Calculate the pH after the addition of the following volumes of NaOH:
(a) 0.0 mL

 Verified step by step guidance
Verified step by step guidance

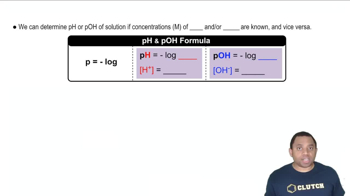

A 100.0 mL sample of a solution that is 0.100 M in HCl and 0.100 M in HCN is titrated with 0.100 M NaOH. Calculate the pH after the addition of the following volumes of NaOH:
(a) 0.0 mL
Calculate the pH of solutions prepared by:
(d) Mixing equal volumes of 0.20 M HCl and 0.50 M HNO3.
(Assume that volumes are additive.)
What is the pH and the principal source of H3O+ ions in 1.0 * 10-10 M HCl? (Hint: The pH of an acid solution can’t exceed 7.) What is the pH of 1.0 * 10-7 M HCl?
A 40.0 mL sample of a mixture of HCl and H3PO4 was titrated with 0.100 M NaOH. The first equivalence point was reached after 88.0 mL of base, and the second equivalence point was reached after 126.4 mL of base.
(e) Sketch the pH titration curve, and label the buffer regions and equivalence points.
The following pictures represent aqueous solutions of three acids HA1A = X, Y, or Z2; water molecules have been omitted for clarity.
(c) Which acid, if any, is a strong acid?