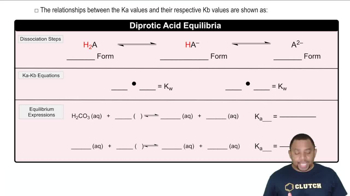
Like sulfuric acid, selenic acid H2SeO4 is a diprotic acid that has a very large value of Ka1. Calculate the pH and the concentrations of all species present in 0.50 M H2SeO4 (Ka2 = 1.2 * 10^-22).

Diprotic acids are acids that can donate two protons (H⁺ ions) per molecule in an aqueous solution. This characteristic allows them to undergo two dissociation steps, each with its own acid dissociation constant (Ka). Understanding the behavior of diprotic acids is crucial for calculating pH and species concentrations, as each step influences the overall acidity and the resulting equilibrium concentrations.

The acid dissociation constant (Ka) quantifies the strength of an acid in solution, representing the equilibrium between the undissociated acid and its ions. A larger Ka value indicates a stronger acid that dissociates more completely. For diprotic acids, both dissociation steps have distinct Ka values, which are essential for determining the concentrations of all species in solution, especially when calculating pH.

pH is a measure of the hydrogen ion concentration in a solution, calculated using the formula pH = -log[H⁺]. For strong acids, the pH can often be determined directly from the concentration of the acid, while for weak acids, it requires consideration of the dissociation constants. In the case of diprotic acids like selenic acid, both dissociation steps must be accounted for to accurately calculate the pH and the concentrations of all species present.