A 7.0 mass % solution of H3PO4 in water has a density of1.0353 g/mL. Calculate the pH and the molar concentrationsof all species present (H3PO4, H2PO4-, PO43-, H3O+ ,and OH-) in the solution. Values of equilibrium constantsare listed in Appendix C.

Verified step by step guidance

Identify the given information: The solution is 7.0 mass % H3PO4 with a density of 1.0353 g/mL.

Calculate the mass of H3PO4 in 1 liter of solution: Use the density to find the total mass of the solution, then apply the mass percentage to find the mass of H3PO4.

Convert the mass of H3PO4 to moles: Use the molar mass of H3PO4 to convert the mass to moles.

Set up the equilibrium expressions: Use the equilibrium constants (Ka1, Ka2, and Ka3) for the dissociation of H3PO4 to find the concentrations of H2PO4^-, PO4^3-, H3O^+, and OH^-.

Calculate the pH: Use the concentration of H3O^+ to find the pH of the solution.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

16m

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Concentration and Molarity

Concentration refers to the amount of solute present in a given volume of solution. Molarity, a common unit of concentration, is defined as moles of solute per liter of solution (mol/L). To calculate molarity from mass percent, one must first determine the mass of solute in a specific volume of solution, which can be derived from the solution's density.

Acid-Base Equilibria

Acid-base equilibria involve the dissociation of acids and bases in solution, which can be described using equilibrium constants (Ka for acids and Kb for bases). For phosphoric acid (H3PO4), it can lose protons in a stepwise manner, leading to the formation of various species such as H2PO4- and PO43-. Understanding these equilibria is essential for calculating the concentrations of all species in the solution.

pH and pOH Calculations

pH is a measure of the hydrogen ion concentration in a solution, calculated as pH = -log[H3O+]. The pOH, which measures hydroxide ion concentration, is related to pH by the equation pH + pOH = 14 at 25°C. To find the pH of the solution, one must first determine the concentration of H3O+ ions, which can be derived from the dissociation of H3PO4 and the equilibrium constants provided.

Recommended video:

Guided course

02:09

pH and pOH Calculations

Related Practice

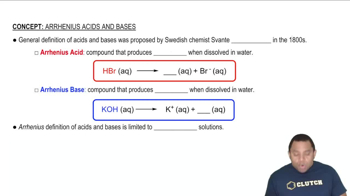
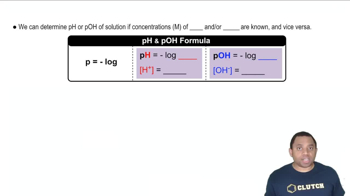
Textbook Question

Acid and base behavior can be observed in solvents other than water. One commonly used solvent is dimethyl sulfoxide (DMSO), which can be treated as a monoprotic acid 'HSol.' Just as water can behave either as an acid or a base, so HSol can behave either as a Brønsted–Lowry acid or base. (b) The weak acid HCN has an acid dissociation constant Ka = 1.3 * 10-13 in the solvent HSol. If 0.010 mol of NaCN is dissolved in 1.00 L of HSol, what is the equilibrium concentration of H2Sol + ?

Textbook Question

In the case of very weak acids, 3H3O+ 4 from the dissociation of water is significant compared with 3H3O+ 4 from the dissociation of the weak acid. The sugar substitute saccharin 1C7H5NO3S2, for example, is a very weak acid having Ka = 2.1 * 10-12 and a solubility in water of 348 mg/100 mL. Calculate 3H3O+ 4 in a saturated solution of saccharin. (Hint: Equilibrium equations for the dissociation of saccharin and water must be solved simultaneously.)

Textbook Question

In aqueous solution, sodium acetate behaves as a strong electrolyte, yielding Na+ cations and CH3CO2 - anions. A particular solution of sodium acetate has a pH of 9.07 and a density of 1.0085 g/mL. What is the molality of this solution, and what is its freezing point?

Textbook Question

During a certain time period, 4.0 million tons of SO₂ were released into the atmosphere and subsequently oxidized to SO₃. As explained in the Inquiry, the acid rain produced when the SO₃ dissolves in water can damage marble statues: CaCO₃(s) + H₂SO₄(aq) → CaSO₄(aq) + CO₂(g) + H₂O(l) (a) How many 500 pound marble statues could be damaged by the acid rain? (Assume that the statues are pure CaCO₃ and that a statue is damaged when 3.0% of its mass is dissolved.)