What is the value of the van’t Hoff factor for KCl if a 1.00 m aqueous solution shows a vapor pressure depression of 0.734 mm Hg at 298 K? (The vapor pressure of water at 298 K is 23.76 mm Hg.)

Verified step by step guidance

Identify the formula for vapor pressure depression: \( \Delta P = i \cdot m \cdot K_f \), where \( \Delta P \) is the vapor pressure depression, \( i \) is the van’t Hoff factor, \( m \) is the molality, and \( K_f \) is the cryoscopic constant. However, since we are dealing with vapor pressure, we use \( \Delta P = i \cdot m \cdot P^0 \), where \( P^0 \) is the vapor pressure of the pure solvent.

Calculate the vapor pressure depression \( \Delta P \) using the given values: \( \Delta P = P^0 - P_{solution} = 23.76 \text{ mm Hg} - (23.76 \text{ mm Hg} - 0.734 \text{ mm Hg}) \).

Substitute the known values into the vapor pressure depression formula: \( 0.734 \text{ mm Hg} = i \cdot 1.00 \text{ m} \cdot 23.76 \text{ mm Hg} \).

Solve for the van’t Hoff factor \( i \) by rearranging the equation: \( i = \frac{0.734 \text{ mm Hg}}{1.00 \text{ m} \cdot 23.76 \text{ mm Hg}} \).

Interpret the result: The van’t Hoff factor \( i \) represents the number of particles the solute dissociates into in solution. For KCl, which dissociates into K\(^+\) and Cl\(^-\), the theoretical value of \( i \) should be close to 2.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

van't Hoff Factor (i)

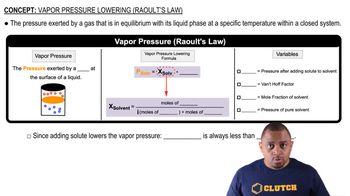
The van't Hoff factor (i) is a measure of the number of particles into which a solute dissociates in solution. For ionic compounds like KCl, which dissociates into K+ and Cl- ions, the van't Hoff factor is typically 2. This factor is crucial for calculating colligative properties, such as vapor pressure depression, as it directly influences the extent of these properties based on the number of solute particles present.

Vapor Pressure Depression

Vapor pressure depression occurs when a non-volatile solute is added to a solvent, resulting in a decrease in the solvent's vapor pressure. This phenomenon is a colligative property, meaning it depends on the number of solute particles rather than their identity. The extent of vapor pressure depression can be calculated using Raoult's Law, which relates the vapor pressure of the solution to the mole fraction of the solvent.

Raoult's Law

Raoult's Law states that the vapor pressure of a solvent in a solution is equal to the vapor pressure of the pure solvent multiplied by its mole fraction in the solution. This law is fundamental in understanding how the addition of solute affects the vapor pressure of the solvent. In the context of the question, it allows for the calculation of the van't Hoff factor by relating the observed vapor pressure depression to the concentration of the solute.

Recommended video:

Guided course

02:40

Raoult's Law and Vapor Pressure

Related Practice

Textbook Question

The van't Hoff factor for CaCl2 is 2.71. What is its mass % in an aqueous solution that has Tf = - 1.14 °C?

Textbook Question

A solid mixture of KCl, KNO3, and Ba1NO322 is20.92 mass % chlorine, and a 1.000 g sample of the mix- ture in 500.0 mL of aqueous solution at 25 °C has an osmotic pressure of 744.7 mm Hg. What are the mass percents of KCl, KNO3, and Ba1NO322 in the mixture?

Textbook Question

A solution of LiCl in a mixture of water and methanol 1CH3OH2 has a vapor pressure of 39.4 mm Hg at 17 °C and 68.2 mm Hg at 27 °C. The vapor pressure of pure water is 14.5 mm Hg at 17 °C and 26.8 mm Hg at 27 °C, and the vapor pressure of pure methanol is 82.5 mm Hg at 17 °C and 140.3 mm Hg at 27 °C. What is the composition of the solution in mass percent?

Textbook Question

At 60 °C, compound X has a vapor pressure of 96 mm Hg, benzene 1C6H62 has a vapor pressure of 395 mm Hg, and a 50:50 mixture by mass of benzene and X has a vapor pres- sure of 299 mm Hg. What is the molar mass of X?