
Nitrogen dioxide dimerizes to give dinitrogen tetroxide: 2 NO2(g) ⇌ N2O4(g). At 298 K, 9.66 g of an NO2 and N2O4 mixture exerts a pressure of 0.487 atm in a volume of 6.51 L. What are the mole fractions of the two gases in the mixture?
 Verified step by step guidance
Verified step by step guidanceKey Concepts
Ideal Gas Law

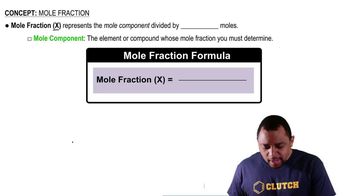
Mole Fraction
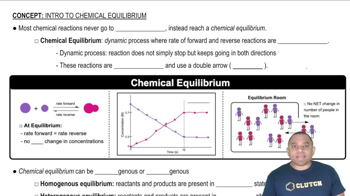
Chemical Equilibrium
A steel container with a volume of 500.0 mL is evacuated, and 25.0 g of CaCO3 is added. The container and contents are then heated to 1500 K, causing the CaCO3 to decompose completely, according to the equation CaCO3(s) → CaO(s) + CO2(g). (a) Using the ideal gas law and ignoring the volume of any solids remaining in the container, calculate the pressure inside the container at 1500 K.
A steel container with a volume of 500.0 mL is evacuated, and 25.0 g of CaCO3 is added. The container and contents are then heated to 1500 K, causing the CaCO3 to decompose completely, according to the equation CaCO3(s) → CaO(s) + CO2(g). (b) Now make a more accurate calculation of the pressure inside the container. Take into account the volume of solid CaO (density = 3.34 g/mL) in the container, and use the van der Waals equation to calculate the pressure. The van der Waals constants for CO2(g) are a = 3.59 (L2-atm)/mol2 and b = 0.0427 L/mol.
An empty 4.00-L steel vessel is filled with 1.00 atm of CH4(g) and 4.00 atm of O2(g) at 300 °C. A spark causes the CH4 to burn completely, according to the equation
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g) ΔH° = -802 kJ
(a) What mass of CO2(g) is produced in the reaction?
An empty 4.00-L steel vessel is filled with 1.00 atm of CH4(g) and 4.00 atm of O2(g) at 300 °C. A spark causes the CH4 to burn completely, according to the equation
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g) ΔH° = -802 kJ
(b) What is the final temperature inside the vessel after combustion, assuming that the steel vessel has a mass of 14.500 kg, the mixture of gases has an average molar heat capacity of 21 J/(mol·°C), and the heat capacity of steel is 0.449 J/(g·°C)?
An empty 4.00-L steel vessel is filled with 1.00 atm of CH4(g) and 4.00 atm of O2(g) at 300 °C. A spark causes the CH4 to burn completely, according to the equation
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g) ΔH° = -802 kJ
(c) What is the partial pressure of CO2(g) in the vessel after combustion?
