A gas mixture for use in some lasers contains 5.00% by weight HCl, 1.00% H2, and 94% Ne. The mixture is sold in cylinders that have a volume of 49.0 L and a pressure of 13,800 kPa at 210 °C. What is the partial pressure in kilopascals of each gas in the mixture?

Dalton's Law states that in a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of each individual gas. Each gas's partial pressure can be calculated using the formula: P_total = P_HCl + P_H2 + P_Ne, where P represents the partial pressure of each gas. This law is fundamental for understanding how gases behave in mixtures.

The Ideal Gas Law, represented as PV = nRT, relates the pressure (P), volume (V), number of moles (n), the ideal gas constant (R), and temperature (T) of a gas. This equation allows us to calculate the number of moles of gas in a mixture, which is essential for determining the partial pressures of each component in the gas mixture based on their mole fractions.

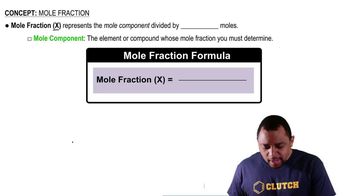
Mole fraction is a way of expressing the concentration of a component in a mixture, defined as the ratio of the number of moles of that component to the total number of moles of all components. It is crucial for calculating partial pressures, as the partial pressure of each gas can be found by multiplying its mole fraction by the total pressure of the gas mixture.