A stellar object is emitting radiation at 3.55 mm. a. What type of electromagnetic spectrum is this radiation? b. If a detector is capturing 3.2×108 photons per second at this wavelength, what is the total energy of the photons detected in 1.0 hour?

Molybdenum metal must absorb radiation with a minimum frequency of 1.09 * 1015 s - 1 before it can eject an electron from its surface via the photoelectric effect. (c) If molybdenum is irradiated with light of wavelength of 120 nm, what is the maximum possible kinetic energy of the emitted electrons?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Photoelectric Effect
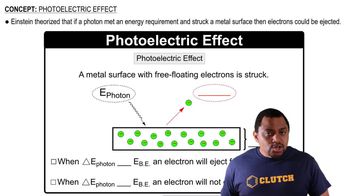
Energy-Frequency Relationship
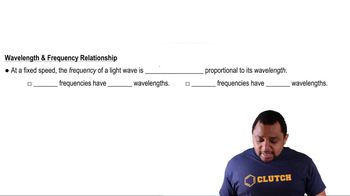
Kinetic Energy of Emitted Electrons

Molybdenum metal must absorb radiation with a minimum frequency of 1.09 * 1015 s - 1 before it can eject an electron from its surface via the photoelectric effect. (a) What is the minimum energy needed to eject an electron?
Molybdenum metal must absorb radiation with a minimum frequency of 1.09 * 1015 s - 1 before it can eject an electron from its surface via the photoelectric effect. (b) What wavelength of radiation will provide a photon of this energy?
Does the hydrogen atom 'expand' or 'contract' when an electron is excited from the n = 1 state to the n = 3 state?
Classify each of the following statements as either true or false: (a) A hydrogen atom in the n = 3 state can emit light at only two specific wavelengths (b) a hydrogen atom in the n = 2 state is at a lower energy than one in the n = 1 state (c) the energy of an emitted photon equals the energy difference of the two states involved in the emission.
