Skip to main content
Pearson+ LogoPearson+ Logo
Ch.23 - Transition Metals and Coordination Chemistry
All textbooksBrown 15th EditionCh.23 - Transition Metals and Coordination ChemistryProblem 79
Chapter 23, Problem 79

Complete the exercises below. Which of the following objects is chiral: a. a left shoe, b. a slice of bread, c. a wood screw, d. a molecular model of Zn(en)Cl₂, e. a typical golf club?

Verified step by step guidance
1
Step 1: Understand the concept of chirality. Chirality refers to an object that cannot be superimposed on its mirror image. A chiral object and its mirror image are non-identical, much like left and right hands.
Step 2: Analyze each object for symmetry. A chiral object lacks an internal plane of symmetry, meaning it does not have a mirror plane that divides it into two identical halves.
Step 3: Evaluate object (a) - a left shoe. Consider if a left shoe can be superimposed on its mirror image, which would be a right shoe. Since they are not identical, a left shoe is chiral.
Step 4: Evaluate object (b) - a slice of bread. Typically, a slice of bread is symmetrical and can be superimposed on its mirror image, making it achiral.
Step 5: Evaluate object (c) - a wood screw. Consider the helical structure of a screw. If the screw has a right-handed or left-handed twist, it is chiral because its mirror image would have the opposite twist.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Chirality

Chirality is a property of asymmetry important in several branches of science, particularly in chemistry. An object is considered chiral if it cannot be superimposed on its mirror image, meaning it has a non-superimposable mirror image. This concept is crucial in understanding molecular structures, especially in organic chemistry, where chiral molecules can exhibit different properties and behaviors.
Recommended video:
Guided course
02:37
Chirality

Enantiomers

Enantiomers are a type of stereoisomer that are mirror images of each other but cannot be superimposed. They often have identical physical properties except for their interaction with polarized light and reactions in chiral environments, such as biological systems. Understanding enantiomers is essential for grasping the implications of chirality in pharmaceuticals and biochemistry.
Recommended video:
Guided course
02:33
Drawing Enantiomers

Symmetry in Objects

Symmetry plays a critical role in determining chirality. An object is achiral if it possesses a plane of symmetry, meaning it can be divided into two identical halves. In contrast, chiral objects lack such symmetry, making them unique in their spatial arrangement. Recognizing symmetry helps in identifying chiral versus achiral objects in various contexts, including molecular models and everyday items.
Recommended video:
Guided course
01:50
Density of Geometric Objects
Related Practice
Textbook Question

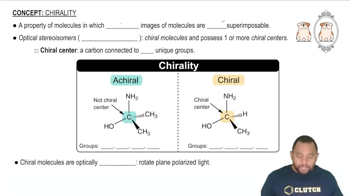
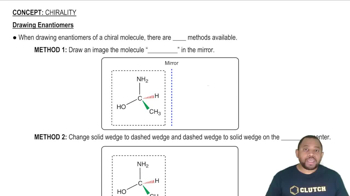
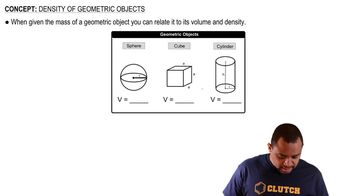
The molecule dimethylphosphinoethane [(CH3)2PCH2CH2P(CH3)2, which is abbreviated dmpe] is used as a ligand for some complexes that serve as catalysts. A complex that contains this ligand is Mo(CO)4(dmpe) .

a. Draw the Lewis structure for dmpe, and compare it with ethylenediamine as a coordinating ligand.

b. What is the oxidation state of Mo in Na2[Mo(CN)2(CO)2(dmpe)] ?

c. Sketch the structure of the [Mo(CN)2(CO)2(dmpe)]2- ion, including all the possible isomers.

Textbook Question

Carbon monoxide, CO, is an important ligand in coordination chemistry. When CO is reacted with nickel metal, the product is [Ni(CO)4] which is a toxic, pale yellow liquid.

a. What is the oxidation number for nickel in this compound?

b. Given that [Ni(CO)4] is a diamagnetic molecule with a tetrahedral geometry, what is the electron configuration of nickel in this compound?

c. Write the name for [Ni(CO)4] using the nomenclature rules for coordination compounds.