Textbook Question
The atomic masses of hydrogen-2 (deuterium), helium-4, and lithium-6 are 2.014102 amu, 4.002602 amu, and 6.0151228 amu, respectively. For each isotope, calculate
(c) the nuclear binding energy per nucleon.
Ch.21 - Nuclear Chemistry
Chapter 21, Problem 51
The energy from solar radiation falling on Earth is 1.07 * 10^16 kJ/min. (a) How much loss of mass from the Sun occurs in one day from just the energy falling on Earth? (b) If the energy released in the reaction 235U + 10n → 14156Ba + 9236Kr + 310n (235U nuclear mass, 234.9935 amu; 141Ba nuclear mass, 140.8833 amu; 92Kr nuclear mass, 91.9021 amu) is taken as typical of that occurring in a nuclear reactor, what mass of uranium-235 is required to equal 0.10% of the solar energy that falls on Earth in 1.0 day?
Verified step by step guidance1
Step 1: Calculate the total energy from solar radiation falling on Earth in one day. Since the energy is given as 1.07 \times 10^{16} \text{kJ/min}, multiply this by the number of minutes in a day (1440 minutes) to find the total energy in kJ.
Step 2: Use Einstein's mass-energy equivalence principle, E=mc^2, to find the mass loss from the Sun. Rearrange the formula to solve for mass (m = E/c^2), where E is the energy calculated in Step 1 and c is the speed of light (3.00 \times 10^8 \text{m/s}).
Step 3: Calculate the energy released in the nuclear reaction of 235U. First, find the mass defect by subtracting the total mass of the products (141Ba, 92Kr, and 3 neutrons) from the mass of the reactants (235U and 1 neutron). Convert the mass defect from amu to kg using the conversion factor 1 amu = 1.660539 \times 10^{-27} \text{kg}.
Step 4: Convert the mass defect to energy using E=mc^2, where m is the mass defect in kg and c is the speed of light. This will give the energy released per reaction in joules.
Step 5: Determine the mass of uranium-235 required to produce 0.10% of the solar energy falling on Earth in one day. First, calculate 0.10% of the total solar energy from Step 1. Then, divide this energy by the energy per reaction from Step 4 to find the number of reactions needed. Finally, multiply the number of reactions by the molar mass of 235U (235.0439299 g/mol) to find the mass of uranium-235 required.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Mass-Energy Equivalence
Mass-energy equivalence, expressed by Einstein's equation E=mc², states that mass can be converted into energy and vice versa. This principle is crucial for understanding how energy loss from the Sun translates into mass loss. In the context of the question, the energy from solar radiation can be used to calculate the corresponding mass loss from the Sun over a specified time period.
Recommended video:
Guided course
04:12
Energy to Mass Conversion
Nuclear Reactions and Energy Release
Nuclear reactions, such as the fission of uranium-235, release significant amounts of energy due to the conversion of mass into energy. The specific reaction provided in the question illustrates how the mass of the reactants is greater than the mass of the products, with the difference released as energy. Understanding this concept is essential for calculating the mass of uranium-235 needed to match a given energy output.
Recommended video:
Guided course
02:06Nuclear Binding Energy
Energy Conversion and Units
Energy conversion involves changing energy from one form to another, and it is important to be consistent with units when performing calculations. In this question, solar energy is given in kJ/min, while nuclear energy is typically expressed in joules or MeV. Converting these units appropriately is necessary to accurately compare the energy from solar radiation with the energy released in nuclear reactions.
Recommended video:
Guided course
01:56Conversion Factors
Related Practice
Textbook Question
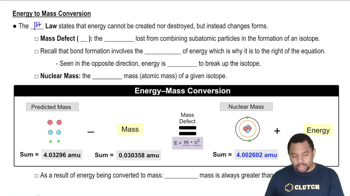
The atomic masses of nitrogen-14, titanium-48, and xenon-129 are 13.999234 amu, 47.935878 amu, and 128.904779 amu, respectively. For each isotope, calculate (a) the nuclear mass.
Textbook Question
Based on the following atomic mass values: 1H, 1.00782 amu; 2H, 2.01410 amu; 3H, 3.01605 amu; 3He, 3.01603 amu; 4He, 4.00260 amu—and the mass of the neutron given in the text, calculate the energy released per mole in each of the following nuclear reactions, all of which are possibilities for a controlled fusion process:
(a) 21H + 31H → 42He + 10n
(b) 21H + 21H → 32He + 10n
(c) 21H + 32He → 42He + 11H
1
views
Textbook Question
Iodine-131 is a convenient radioisotope to monitor thyroid activity in humans. It is a beta emitter with a half-life of 8.02 days. The thyroid is the only gland in the body that uses iodine. A person undergoing a test of thyroid activity drinks a solution of NaI, in which only a small fraction of the iodide is radioactive. b. A normal thyroid will take up about 12% of the ingested iodide in a few hours. How long will it take for the radioactive iodide taken up and held by the thyroid to decay to 0.01% of the original amount?