Ch.21 - Nuclear Chemistry
Chapter 21, Problem 88
Naturally found uranium consists of 99.274% 238U, 0.720% 235U, and 0.006% 234U. As we have seen, 235U is the isotope that can undergo a nuclear chain reaction. Most of the 235U used in the first atomic bomb was obtained by gaseous diffusion of uranium hexafluoride, UF6(g). (a) What is the mass of UF6 in a 30.0-L vessel of UF6 at a pressure of 695 torr at 350 K? (b) What is the mass of 235U in the sample described in part (a)? (c) Now suppose that the UF6 is diffused through a porous barrier and that the change in the ratio of 238U and 235U in the diffused gas can be described by Equation 10.23. What is the mass of 235U in a sample of the diffused gas analogous to that in part (a)? (d) After one more cycle of gaseous diffusion, what is the percentage of 235UF6 in the sample?
Verified step by step guidance1
Step 1: To find the mass of UF6 in a 30.0-L vessel at 695 torr and 350 K, use the ideal gas law: PV = nRT. Convert the pressure from torr to atm by dividing by 760. Use R = 0.0821 L·atm/mol·K for the gas constant.
Step 2: Solve the ideal gas law equation for n (number of moles): n = PV / RT. Substitute the values for P (in atm), V (30.0 L), R, and T (350 K) to find n.
Step 3: Calculate the molar mass of UF6. The molar mass of uranium (U) is approximately 238 g/mol, and the molar mass of fluorine (F) is approximately 19 g/mol. Since there are six fluorine atoms, the molar mass of UF6 is 238 + 6(19).
Step 4: Multiply the number of moles of UF6 (n) by the molar mass of UF6 to find the mass of UF6 in the vessel.
Step 5: To find the mass of 235U in the UF6 sample, calculate the fraction of 235U in natural uranium (0.720%) and apply it to the mass of UF6. Consider the molar mass of 235U when calculating its mass in the sample.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Ideal Gas Law
The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law is essential for calculating the mass of UF6 in the given vessel, as it allows us to determine the number of moles of gas present under specific conditions of pressure and temperature.
Recommended video:
Guided course
01:15
Ideal Gas Law Formula
Isotopes and Atomic Mass
Isotopes are variants of a chemical element that have the same number of protons but different numbers of neutrons, resulting in different atomic masses. Understanding the composition of naturally occurring uranium, particularly the proportions of 238U and 235U, is crucial for calculating the mass of 235U in the UF6 sample.
Recommended video:
Guided course
02:19Atomic Mass
Gaseous Diffusion
Gaseous diffusion is the process by which gas molecules move from an area of higher concentration to an area of lower concentration through a porous barrier. This concept is important for understanding how the ratio of isotopes changes during the diffusion of UF6, which affects the mass of 235U in the diffused gas and subsequent calculations.
Recommended video:
Guided course
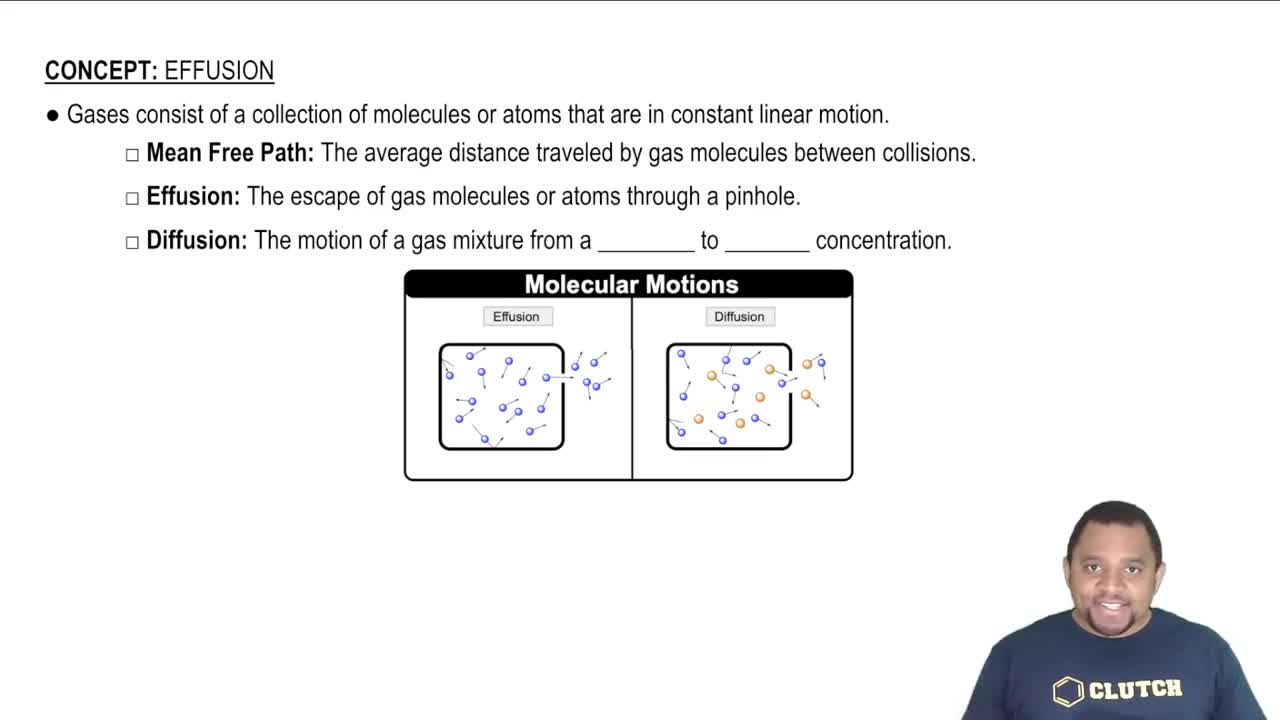
01:31Effusion vs Diffusion
Related Practice