Textbook Question
Complete and balance the following nuclear equations by supplying the missing particle: (b) 21H + 32He → 42He + ?
1
views
Ch.21 - Nuclear Chemistry
Chapter 21, Problem 29e
Complete and balance the following nuclear equations by supplying the missing particle: (e) 5926Fe → 0-1e + ?
Verified step by step guidance1
Step 1: Understand that in a nuclear equation, the sum of the atomic numbers (the lower number) and the sum of the atomic masses (the upper number) must be the same on both sides of the equation.
Step 2: Identify the atomic number and atomic mass of the given particle. For 5926Fe, the atomic number is 26 and the atomic mass is 59.
Step 3: Identify the atomic number and atomic mass of the electron (0-1e). The atomic number is -1 and the atomic mass is 0.
Step 4: To balance the equation, find a particle that, when added to the electron, will have an atomic number and atomic mass that add up to those of the original particle. The atomic number should be 26 + 1 = 27 and the atomic mass should be 59 + 0 = 59.
Step 5: The missing particle is therefore 5927Co, because it has an atomic number of 27 and an atomic mass of 59, which balances the equation.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Nuclear Reactions
Nuclear reactions involve changes in an atom's nucleus and can result in the transformation of one element into another. These reactions are governed by the conservation of mass and charge, meaning that the total number of protons and neutrons must remain constant before and after the reaction.
Recommended video:
Guided course
02:06
Nuclear Binding Energy
Beta Decay
Beta decay is a type of radioactive decay in which a neutron in an atomic nucleus is transformed into a proton, emitting a beta particle (an electron or positron) in the process. This transformation increases the atomic number of the element by one while keeping the mass number unchanged, leading to the formation of a new element.
Recommended video:
Guided course
03:01Beta Decay
Balancing Nuclear Equations
Balancing nuclear equations requires ensuring that both the mass number and atomic number are conserved. This means that the sum of the mass numbers and the sum of the atomic numbers on both sides of the equation must be equal, allowing for the identification of any missing particles in the reaction.
Recommended video:
Guided course
01:32Balancing Chemical Equations
Related Practice
Textbook Question
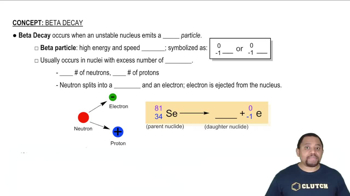
Complete and balance the following nuclear equations by supplying the missing particle: (d) 12253I → 12254Xe + ?
Textbook Question
Complete and balance the following nuclear equations by supplying the missing particle: (a) 147N + 42He¡? + 11H
Textbook Question
Complete and balance the following nuclear equations by supplying the missing particle: (d) 5826Fe + 2 10n¡6027Co + ?
Textbook Question
Complete and balance the following nuclear equations by supplying the missing particle: (e) 23592U + 10n¡13554Xe + 2 10n + ?