At 700 K, the equilibrium constant for the reaction CCl4(𝑔) ⇌ C(𝑠) + 2 Cl2(𝑔) is 𝐾𝑝 = 0.76. A flask is charged with 2.00 atm of CCl4, which then reaches equilibrium at 700 K. (a) What fraction of the CCl4 is converted into C and Cl2?
Ch.15 - Chemical Equilibrium

Brown15th EditionChemistry: The Central ScienceISBN: 9780137542970Not the one you use?Change textbook
Chapter 15, Problem 92d,e
Consider the hypothetical reaction A(𝑔) + 2 B(𝑔) ⇌ 2 C(𝑔), for which 𝐾𝑐 = 0.25 at a certain temperature. A 1.00-L reaction vessel is loaded with 1.00 mol of compound C, which is allowed to reach equilibrium. Let the variable x represent the number of mol/L of compound A present at equilibrium.
(d) The equation from part (c) is a cubic equation (one that has the form ax3 + bx2 + cx + d = 0). In general, cubic equations cannot be solved in closed form. However, you can estimate the solution by plotting the cubic equation in the allowed range of x that you specified in part (b). The point at which the cubic equation crosses the x-axis is the solution.
(e) From the plot in part (d), estimate the equilibrium concentrations of A, B, and C. (Hint: You can check the accuracy of your answer by substituting these concentrations into the equilibrium expression.)
 Verified step by step guidance
Verified step by step guidance1
Identify the initial concentrations of the reactants and products. Initially, the concentration of C is 1.00 M (since 1.00 mol in a 1.00 L vessel), and the concentrations of A and B are 0 M.
Set up the expression for the equilibrium constant, Kc, using the reaction stoichiometry: Kc = \frac{[C]^2}{[A][B]^2}. Substitute the known value of Kc, which is 0.25.
Define the change in concentration using the variable x, where x is the increase in concentration of A at equilibrium. Since the reaction shows that 1 mole of A reacts with 2 moles of B to produce 2 moles of C, the concentration of B will increase by 2x and the concentration of C will decrease by 2x.
Write the equilibrium concentration expressions in terms of x: [A] = x, [B] = 2x, and [C] = 1.00 - 2x.
Substitute these expressions into the equilibrium constant expression and solve for x. This will give the equilibrium concentrations of A, B, and C. Check the accuracy of your solution by substituting these values back into the equilibrium expression to see if it equals 0.25.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
10mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Equilibrium Constant (Kc)
The equilibrium constant (Kc) is a numerical value that expresses the ratio of the concentrations of products to reactants at equilibrium for a given reaction at a specific temperature. For the reaction A(g) + 2B(g) ⇌ 2C(g), Kc = [C]^2 / ([A][B]^2). A Kc value of 0.25 indicates that at equilibrium, the concentration of products is relatively low compared to reactants, suggesting that the reaction favors the reactants.
Recommended video:
Guided course
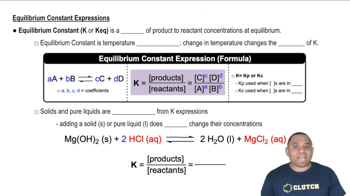
Equilibrium Constant Expressions
ICE Table (Initial, Change, Equilibrium)
An ICE table is a tool used to organize the initial concentrations, the changes in concentrations as the reaction proceeds, and the equilibrium concentrations of reactants and products. By defining initial amounts and using a variable (like x) to represent changes, one can systematically calculate the equilibrium concentrations based on stoichiometry and the equilibrium constant.
Recommended video:
Guided course

ICE Charts and Equilibrium Amount
Stoichiometry in Chemical Reactions
Stoichiometry refers to the quantitative relationship between reactants and products in a chemical reaction, derived from the balanced chemical equation. In the given reaction, the stoichiometric coefficients indicate that one mole of A reacts with two moles of B to produce two moles of C. Understanding these ratios is essential for calculating the changes in concentrations as the system reaches equilibrium.
Recommended video:
Guided course

Stoichiometry Concept
Related Practice
Textbook Question
Textbook Question
At 700 K, the equilibrium constant for the reaction CCl4(𝑔) ⇌ C(𝑠) + 2 Cl2(𝑔) is 𝐾𝑝 = 0.76. A flask is charged with 2.00 atm of CCl4, which then reaches equilibrium at 700 K. (b) What are the partial pressures of CCl4 and Cl2 at equilibrium?
1
views
Textbook Question
At a temperature of 700 K, the forward and reverse rate constants for the reaction 2 HI(g) ⇌ H2(g) + I2(g) are kf = 1.8×10−30 M−1s−1 and kr = 0.063 M−1s−1.
(a) What is the value of the equilibrium constant Kc at 700 K?
(b) Is the forward reaction endothermic or exothermic if the rate constants for the same reaction have values of kf = 0.097M−1s−1 and kr = 2.6 M−1s−1 at 800 K?
