Ch.14 - Chemical Kinetics

Problem 47c

Chapter 14, Problem 47c

Consider the data presented in Exercise 14.19. (c) What is the half-life for the reaction?

Verified step by step guidance

Step 1: Identify the initial concentration of substance C at time t=0, which is 0.045 moles.

Step 2: Determine the concentration of substance C at various time intervals from the table provided.

Step 3: Calculate the time it takes for the concentration of substance C to decrease to half of its initial value (0.045/2 = 0.0225 moles).

Step 4: Compare the calculated half concentration with the values in the table to find the corresponding time.

Step 5: The time at which the concentration of substance C is closest to 0.0225 moles is the half-life of the reaction.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Half-life

Half-life is the time required for the concentration of a reactant to decrease to half of its initial value. In chemical kinetics, it is a crucial concept for understanding the rate of a reaction and is particularly useful for first-order reactions, where the half-life remains constant regardless of the initial concentration.

Reaction Rate

The reaction rate is a measure of how quickly reactants are converted into products in a chemical reaction. It can be expressed in terms of the change in concentration of a reactant or product over time. Understanding the reaction rate is essential for calculating half-lives and predicting how long a reaction will take to reach a certain point.

Integrated Rate Laws

Integrated rate laws relate the concentration of reactants or products to time, allowing for the calculation of concentrations at any given time. For first-order reactions, the integrated rate law can be used to determine the half-life and is expressed as ln([A]0/[A]) = kt, where [A]0 is the initial concentration, [A] is the concentration at time t, and k is the rate constant.

Recommended video:

Guided course

01:52

Rate Law Fundamentals

Related Practice

Textbook Question

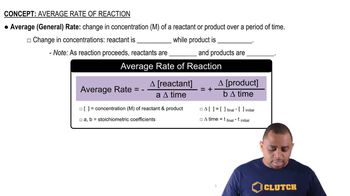
From the following data for the first-order gas-phase isomerization of CH3NC to CH3CN at 215°C, calculate the first-order rate constant and half-life for the reaction:

Time (s) Pressure CH3NC (torr)

0 502

2000 335

5000 180

8000 95.5

12,000 41.7

15,000 22.4

Textbook Question

Consider the data presented in Exercise 14.19. (a) By using appropriate graphs, determine whether the reaction is first order or second order.

Textbook Question

The gas-phase decomposition of NO₂, 2 NO₂(g) → 2 NO(g) + O₂(g), is studied at 383°C, giving the following data:

Time (s) [NO₂] (M)

0.0 0.100

5.0 0.017

10.0 0.0090

15.0 0.0062

20.0 0.0047

(a) Is the reaction first order or second order with respect to the concentration of NO₂?

(c) Predict the reaction rates at the beginning of the reaction for initial concentrations of 0.200 M, 0.100 M, and 0.050 M NO₂.

Textbook Question

Sucrose 1C12H22O112, commonly known as table sugar, reacts in dilute acid solutions to form two simpler sugars, glucose and fructose, both of which have the formula C6H12O6. At 23 C and in 0.5 M HCl, the following data were obtained for the disappearance of sucrose: Time (min) 3C12H22o11 4 1M2 0 0.316 39 0.274 80 0.238 140 0.190 210 0.146 (a) Is the reaction first order or second order with respect to 3C12H22O114?