Here are the essential concepts you must grasp in order to answer the question correctly.
Energy Bands
Energy bands in solids arise from the overlap of atomic orbitals in a crystal lattice, leading to a continuum of energy levels. In metals like copper, these bands allow for the conduction of electricity as electrons can move freely between closely spaced energy levels. Understanding energy bands is crucial for analyzing the electronic properties of materials.
Recommended video:
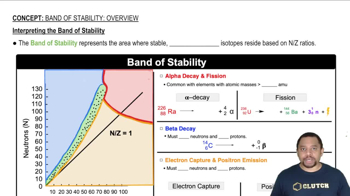
Intepreting the Band of Stability
Energy Level Spacing
The spacing between energy levels in a solid can be approximated by dividing the total range of energy levels by the number of available states, which is often related to the number of atoms in the crystal. This concept is essential for determining how energy is quantized in a material and influences its electrical and thermal properties.
Recommended video:
Crystal Structure
The arrangement of atoms in a crystal, known as its crystal structure, significantly affects its physical properties, including electrical conductivity. In metals like copper, the face-centered cubic (FCC) structure allows for a high density of atoms, contributing to the closely spaced energy levels that define the material's behavior in electronic applications.
Recommended video:

 Verified step by step guidance
Verified step by step guidance