Textbook Question
A particular liquid crystalline substance has the phase diagram shown in the figure. By analogy with the phase diagram for a nonliquid crystalline substance, identify the phase present in each area.
Ch.11 - Liquids and Intermolecular Forces
Chapter 11, Problem 95
Using information in Appendices B and C, calculate the minimum grams of propane, C3H8(g), that must be combusted to provide the energy necessary to convert 5.50 kg of ice at -20 °C to liquid water at 75 °C
Verified step by step guidance1
Step 1: Calculate the total energy required to convert 5.50 kg of ice at -20 °C to liquid water at 75 °C. This process involves three steps: warming the ice to 0 °C, melting the ice, and warming the water to 75 °C. Use the specific heat capacities and heat of fusion for water from Appendix B to calculate the energy for each step and sum them up.
Step 2: Convert the total energy calculated in step 1 from Joules to kilojoules if necessary, as the heat of combustion of propane is usually given in kilojoules per mole.
Step 3: Use the heat of combustion for propane from Appendix C to calculate the number of moles of propane needed to provide the total energy calculated in step 2. Remember that the heat of combustion is the energy released per mole of propane combusted, so divide the total energy by the heat of combustion.
Step 4: Convert the number of moles of propane calculated in step 3 to grams using the molar mass of propane. The molar mass of propane can be calculated by adding up the molar masses of its constituent atoms (3 carbons and 8 hydrogens).
Step 5: The result from step 4 is the minimum grams of propane that must be combusted to provide the necessary energy. Remember that this is a theoretical minimum, and actual combustion processes may be less efficient and require more fuel.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
10mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Thermodynamics of Phase Changes
Understanding the thermodynamics of phase changes is crucial for this problem. It involves calculating the energy required to change the state of a substance, such as melting ice into water and heating it. The specific heat capacity and the heat of fusion are key parameters that quantify the energy needed for these transformations.
Recommended video:
Guided course
01:46
Entropy in Phase Changes
Combustion Reactions
Combustion reactions involve the reaction of a fuel with oxygen to produce energy, typically in the form of heat. For propane (C3H8), the balanced chemical equation shows how much energy is released per mole of propane combusted. This energy release must be calculated to determine how much propane is needed to provide the required energy for the phase change and heating of water.
Recommended video:
Guided course
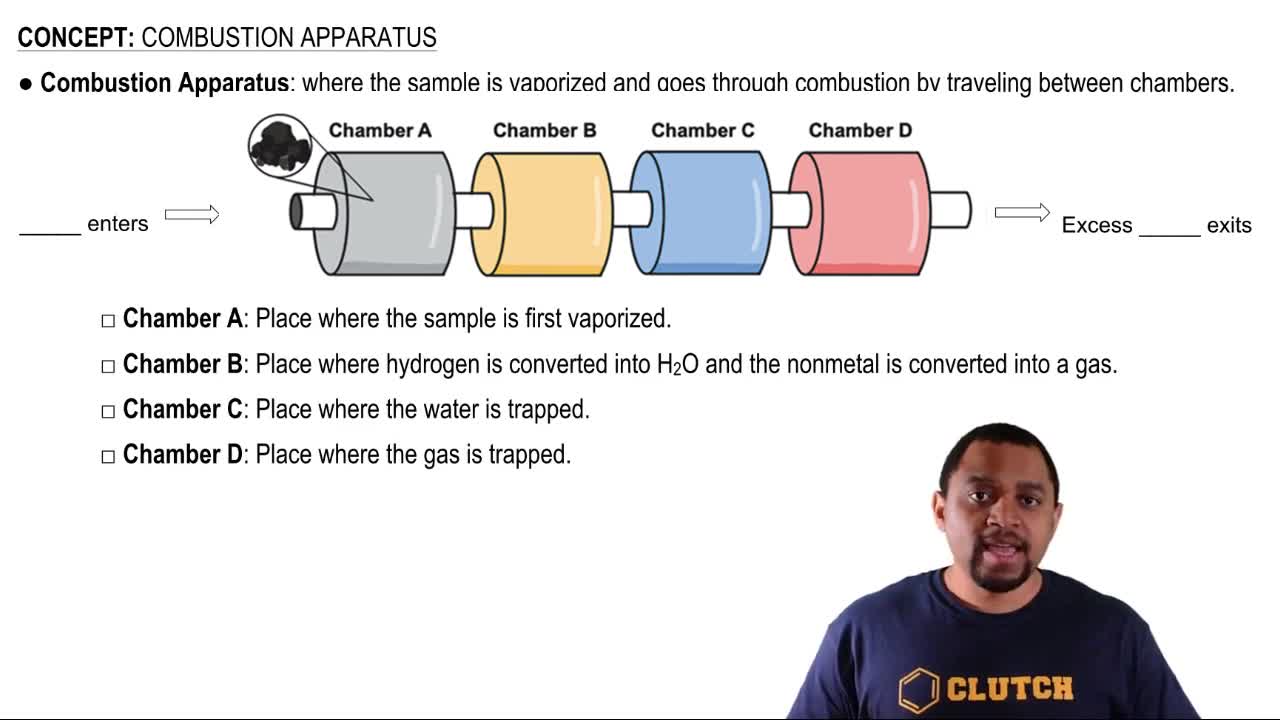
02:24Combustion Apparatus
Stoichiometry
Stoichiometry is the quantitative relationship between reactants and products in a chemical reaction. In this context, it is used to convert the energy required for heating and phase changes into moles of propane needed for combustion. By applying stoichiometric principles, one can relate the energy produced from propane combustion to the energy needed for the ice-to-water conversion.
Recommended video:
Guided course
01:16Stoichiometry Concept
Related Practice
Textbook Question
In Table 11.3, we saw that the viscosity of a series of hydrocarbons increased with molecular weight, doubling from the six-carbon molecule to the ten-carbon molecule.
(a) The eight-carbon hydrocarbon, octane, has an isomer, isooctane. Would you predict that isooctane would have a larger or smaller viscosity than octane? Why?
Textbook Question
The vapor pressure of ethanol (C2H5OH) at 19 °C is 40.0 torr. A 1.00-g sample of ethanol is placed in a 2.00 L container at 19 °C. If the container is closed and the ethanol is allowed to reach equilibrium with its vapor, how many grams of liquid ethanol remain?