Textbook Question
You have a graduated cylinder that contains a liquid (see photograph). Write the volume of the liquid, in milliliters, using the proper number of significant figures.
2
views

 Verified step by step guidance
Verified step by step guidance
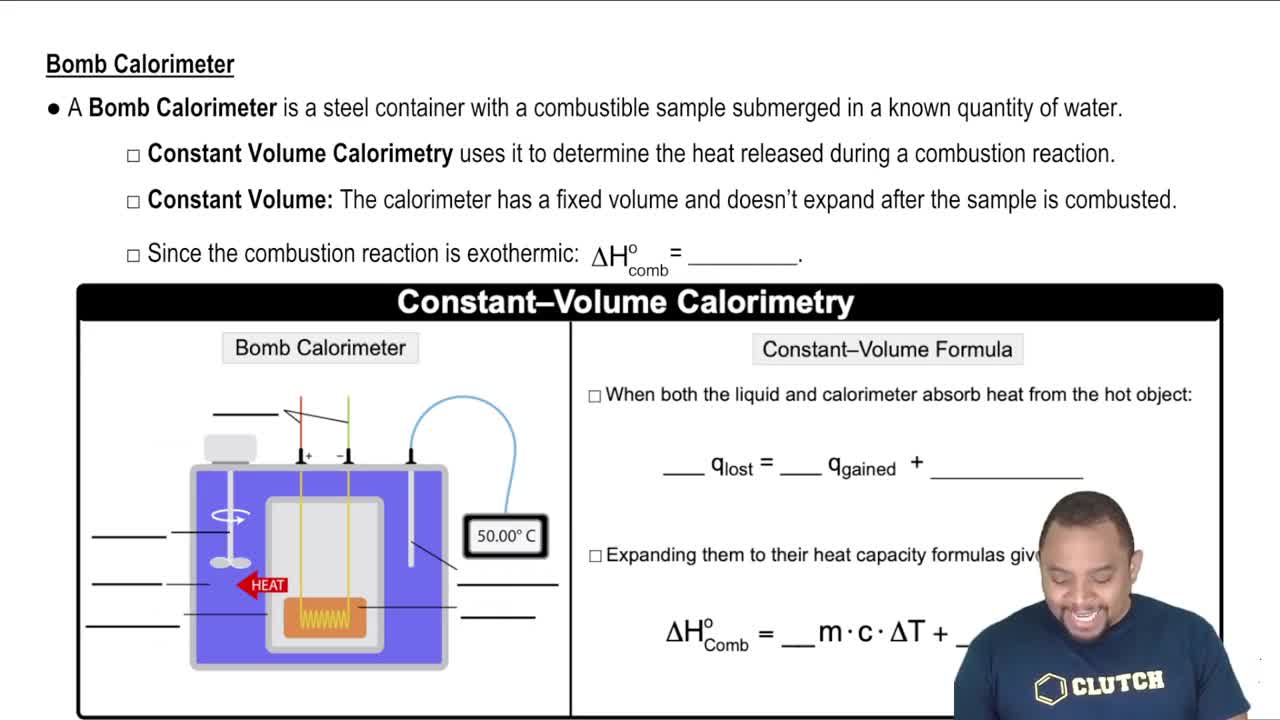


You have a graduated cylinder that contains a liquid (see photograph). Write the volume of the liquid, in milliliters, using the proper number of significant figures.
What are the conversion factors needed to convert the following? c. km to ft
Determine the appropriate conversion factors for the following: c. mi to km
a. A bumblebee flies with a ground speed of 15.2 m/s. Calculate its speed in km/h.
(b) The lung capacity of the blue whale is 5.0×103 L. Convert this volume into gallons.
(d) Bamboo can grow up to 60.0 cm/day. Convert this growth rate into inches per hour.