(b) Carbon dioxide (CO2) is a gas at room temperature and pressure. However, carbon dioxide can be put under pressure to become a 'supercritical fluid' that is a much safer dry-cleaning agent than tetrachloroethylene. At a certain pressure, the density of supercritical CO2 is 0.469 g/cm3. What is the mass of a 25.0-mL sample of supercritical CO2 at this pressure?

c. A cubic piece of metal measures 5.00 cm on each edge. If the metal is nickel, whose density is 8.90 g/cm3, what is the mass of the cube?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Density

Volume of a Cube
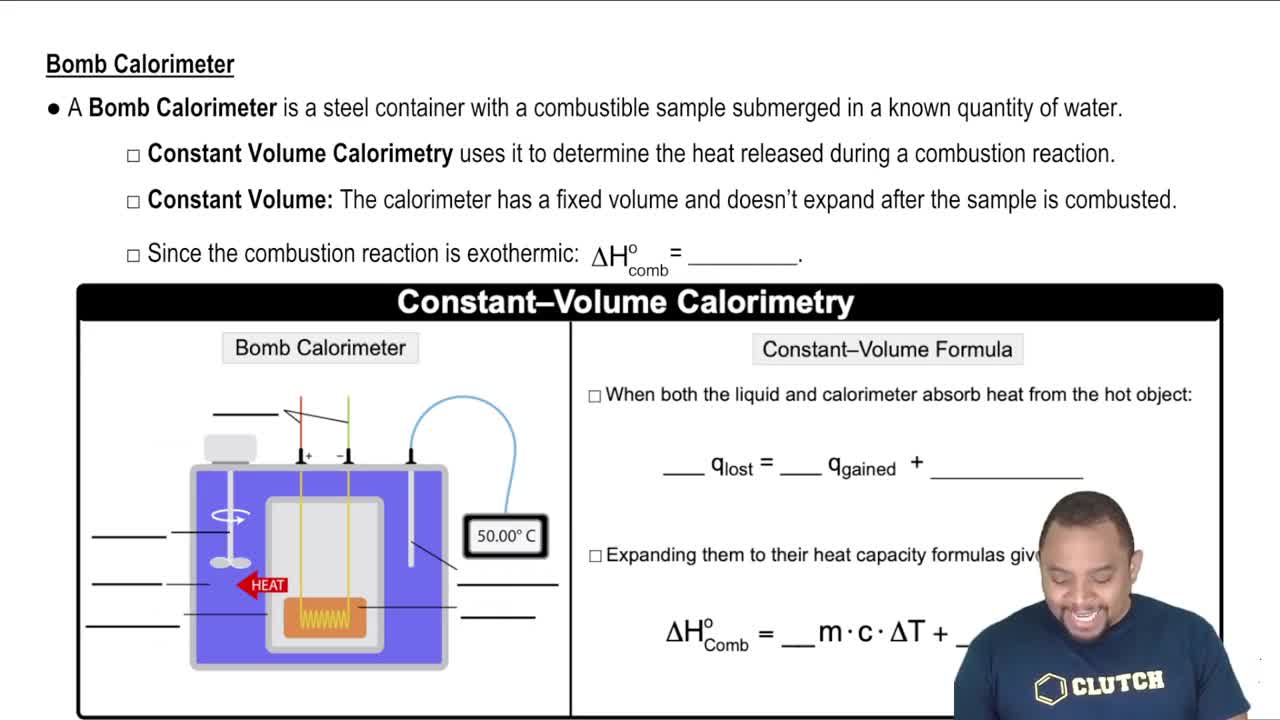
Mass Calculation

(a) To identify a liquid substance, a student determined its density. Using a graduated cylinder, she measured out a 45-mL sample of the substance. She then measured the mass of the sample, finding that it weighed 38.5 g. She knew that the substance had to be either isopropyl alcohol 1density 0.785 g/mL2 or toluene (density 0.866 g/mL). What are the calculated density and the probable identity of the substance?
b. An experiment requires 78.1 g of benzene, a liquid whose density is 0.876 g/mL. Rather than weigh the sample on a balance, a chemist chooses to dispense the liquid using a graduated cylinder. What volume of the liquid should he use?
(d) A cubic piece of metal measures 5.00 cm on each edge. If the metal is nickel, whose density is 8.90 g/cm3, what is the mass of the cube?
a. After the label fell off a bottle containing a clear liquid believed to be a solvent called tetrahydrofuran, a chemist measured the density of the liquid to verify its identity. A 25.0-mL portion of the liquid had a mass of 22.08 g. A chemistry handbook lists the density of tetrahydrofuran at 25 °C as 0.8833 g/mL. Is the calculated density in agreement with the tabulated value?
b. An experiment requires 50.0 g of a substance called n-hexane, whose density at 25 °C is 0.6606 g/mL. What volume of n-hexane should be used?
