Four possible electron configurations for a nitrogen atom are shown below, but only one schematic represents the correct configuration for a nitrogen atom in its ground state. Which configurations violate the Pauli exclusion principle?
Ch.6 - Electronic Structure of Atoms

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 6, Problem 14
Carbon dioxide in the atmosphere absorbs energy in the 4.0–4.5 mm range of the spectrum. (a) Calculate the frequency of the 4.0 mm radiation.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the relationship between wavelength and frequency. The speed of light (c) is related to wavelength (\( \lambda \)) and frequency (\( \nu \)) by the equation \( c = \lambda \nu \).
Step 2: Identify the given values. The wavelength (\( \lambda \)) is given as 4.0 mm. Convert this wavelength from millimeters to meters for consistency with the speed of light units. Recall that 1 mm = 1 \times 10^{-3} m.
Step 3: Use the speed of light constant. The speed of light (c) is approximately \( 3.00 \times 10^8 \) meters per second.
Step 4: Rearrange the equation to solve for frequency (\( \nu \)). The formula becomes \( \nu = \frac{c}{\lambda} \).
Step 5: Substitute the values into the equation. Use the converted wavelength in meters and the speed of light to calculate the frequency.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Electromagnetic Spectrum
The electromagnetic spectrum encompasses all types of electromagnetic radiation, which vary in wavelength and frequency. The range of 4.0 mm falls within the infrared region of the spectrum, where radiation is primarily associated with thermal energy. Understanding the position of this wavelength helps in analyzing how different gases, like carbon dioxide, interact with infrared radiation.
Recommended video:
Guided course
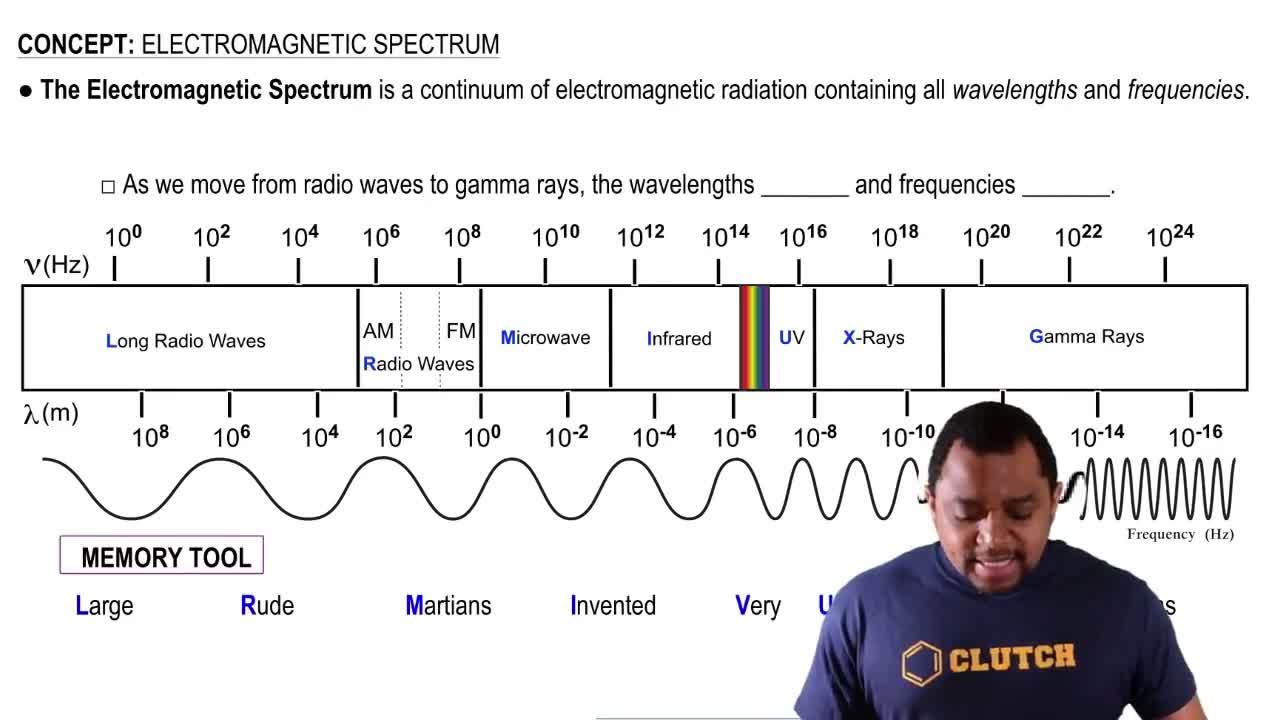
Electromagnetic Spectrum
Wavelength and Frequency Relationship
Wavelength and frequency are inversely related properties of electromagnetic waves, described by the equation c = λν, where c is the speed of light, λ is the wavelength, and ν is the frequency. This relationship allows us to calculate the frequency of radiation when the wavelength is known. For example, to find the frequency of 4.0 mm radiation, one would convert the wavelength to meters and apply the equation.
Recommended video:
Guided course
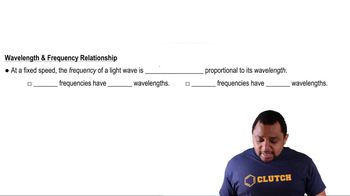
Frequency-Wavelength Relationship
Units of Measurement
In physics and chemistry, it is crucial to use consistent units when performing calculations. Wavelength is often measured in meters (m), while frequency is measured in hertz (Hz). Converting millimeters to meters is necessary for accurate calculations, as 1 mm equals 0.001 m. This ensures that the results are in standard SI units, facilitating clear communication and understanding in scientific contexts.
Recommended video:
Guided course

Units of Radiation Measurement
Related Practice
Textbook Question
1
views
1
rank
Textbook Question
State where in the periodic table these elements appear: (a) elements with the valence-shell electron configuration ns2np5 (b) elements that have three unpaired p electrons (c) an element whose valence electrons are 4s24p1 (d) the d-block elements [Section 6.9]
Textbook Question
Label each of the following statements as true or false. For those that are false, correct the statement. (a) Visible light is a form of electromagnetic radiation.
2
views
Textbook Question
Label each of the following statements as true or false. For those that are false, correct the statement. (b) Ultraviolet light has longer wavelengths than visible light.
2
views
