Here are the essential concepts you must grasp in order to answer the question correctly.
Work in Thermodynamics
In thermodynamics, work is defined as the energy transferred when a force is applied over a distance. For gas expansion or compression, work can be calculated using the formula W = -PΔV, where W is work, P is the external pressure, and ΔV is the change in volume. The negative sign indicates that work is done by the system when it expands.
Recommended video:
First Law of Thermodynamics
Pressure-Volume Work
Pressure-volume work occurs when a gas expands or contracts against an external pressure. The work done by the gas during expansion is directly proportional to the pressure exerted and the change in volume. Understanding this relationship is crucial for calculating the work done during processes like breathing, where lung volume changes against atmospheric pressure.
Recommended video:
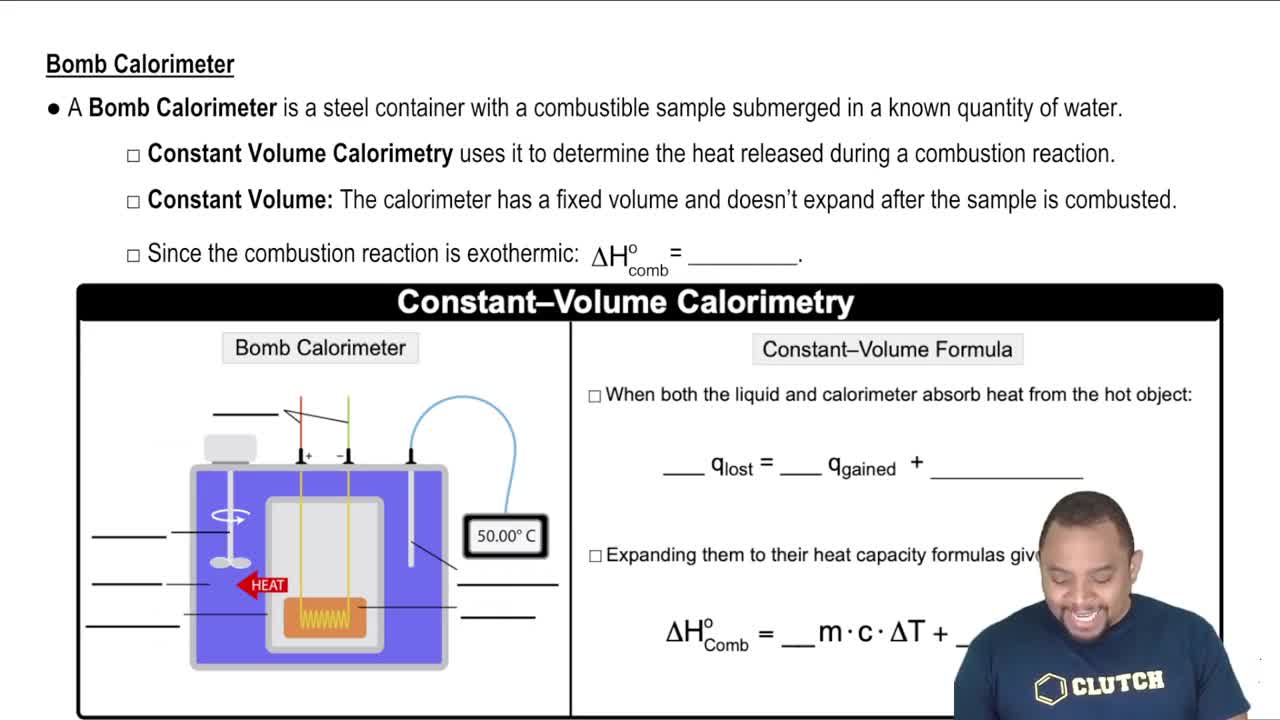
Constant-Volume Calorimetry
Units of Measurement
In this context, work is measured in joules (J), which is the SI unit of energy. One joule is defined as the work done when a force of one newton displaces an object by one meter. It is important to ensure that all units are consistent when performing calculations, particularly when converting pressure from kilopascals to pascals or volume from liters to cubic meters.
Recommended video:
Units of Radiation Measurement