Textbook Question
The lobes of which d orbitals point directly between the ligands in a. octahedral geometry,
Ch.23 - Transition Metals and Coordination Chemistry
Chapter 23, Problem 53
Complete the exercises below. a. Sketch a diagram that shows the definition of the crystal-field splitting energy (∆) for an octahedral crystal-field. b. What is the relationship between the magnitude of ∆ and the energy of the d-d transition for a d¹ complex? c. Calculate ∆ in kJ/mol if a d¹ complex has an absorption maximum at 545 nm.
Verified step by step guidance1
Step 1: For part (a), understand that in an octahedral crystal field, the d-orbitals split into two sets: the lower energy t_{2g} set (d_{xy}, d_{xz}, d_{yz}) and the higher energy e_g set (d_{x^2-y^2}, d_{z^2}). Sketch a diagram showing these orbitals with the energy levels, and label the energy difference between them as the crystal-field splitting energy (∆).
Step 2: For part (b), recognize that the energy of the d-d transition in a d¹ complex is directly related to the crystal-field splitting energy (∆). The energy of the transition corresponds to the energy required to promote an electron from the lower energy t_{2g} orbitals to the higher energy e_g orbitals, which is equal to ∆.
Step 3: For part (c), use the relationship between wavelength (λ) and energy (E) of light, given by the equation E = h*c/λ, where h is Planck's constant (6.626 x 10^{-34} J·s) and c is the speed of light (3.00 x 10^8 m/s). Convert the wavelength from nanometers to meters for calculation.
Step 4: Calculate the energy of the absorbed light in joules using the formula from Step 3. Substitute the given wavelength (545 nm) into the equation to find the energy in joules per photon.
Step 5: Convert the energy from joules per photon to kilojoules per mole by using Avogadro's number (6.022 x 10^{23} mol^{-1}). This will give you the value of ∆ in kJ/mol.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Crystal-Field Theory
Crystal-field theory explains how the arrangement of ligands around a central metal ion affects the energy levels of the d-orbitals. In an octahedral field, the d-orbitals split into two sets: the lower-energy t2g orbitals and the higher-energy eg orbitals. This splitting leads to differences in energy that influence the color and magnetic properties of coordination complexes.
Recommended video:
Guided course
01:18
The study of ligand-metal interactions helped to form Ligand Field Theory which combines CFT with MO Theory.
Crystal-Field Splitting Energy (∆)
Crystal-field splitting energy (∆) is the energy difference between the split d-orbitals in a coordination complex. It is crucial for understanding the electronic transitions that occur when electrons move between these orbitals. The magnitude of ∆ can be influenced by factors such as the nature of the metal ion and the type of ligands surrounding it.
Recommended video:
Guided course
03:04The crystal field splitting pattern for octahedral complexes has the d orbitals on or along the axes as having the higher energy.
d-d Transitions
d-d transitions refer to the electronic transitions between the split d-orbitals in transition metal complexes. For a d¹ complex, the energy of the d-d transition corresponds to the crystal-field splitting energy (∆). The wavelength of light absorbed during this transition can be used to calculate ∆, using the relationship between energy, wavelength, and Planck's equation.
Recommended video:
Guided course
02:06d Orbital Orientations
Related Practice
Textbook Question
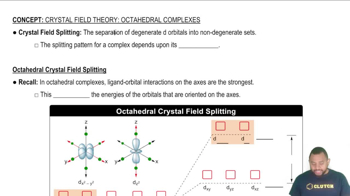
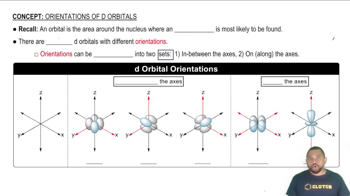
The lobes of which d orbitals point directly between the ligands in b. tetrahedral geometry?
Textbook Question
As shown in Figure 23.26, the d-d transition of [Ti(H2O)6]³⁺ produces an absorption maximum at a wavelength of about 500 nm .
a. What is the magnitude of ∆ for [Ti(H2O)6]³⁺ in kJ/mol?
b. How would the magnitude of ∆ change if the H2O ligands in [Ti(H2O)6]]³⁺ were placed with NH3 ligands?