Write balanced nuclear equations for the following transformations: (d) gold-188 decays by positron emission.

Verified step by step guidance

Identify the initial isotope involved in the decay process. In this case, it is gold-188, which can be represented as

{Au}^{188}

Understand the type of decay occurring. Positron emission involves the conversion of a proton into a neutron, releasing a positron (

e^{0 + 1}

) and a neutrino.

Determine the new element formed after the decay. Since a proton is converted into a neutron, the atomic number decreases by 1. Gold (Au) has an atomic number of 79, so the new element will have an atomic number of 78, which is platinum (Pt).

Write the balanced nuclear equation. The mass number remains the same (188), but the atomic number changes from 79 to 78. The equation is:

{Au}^{188} → {Pt}^{188} + e^{0 + 1}

Verify that the equation is balanced by checking that the sum of the atomic numbers and the sum of the mass numbers are equal on both sides of the equation.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Nuclear Decay

Nuclear decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. This can occur in various forms, including alpha decay, beta decay, and positron emission. In positron emission, a proton in the nucleus is transformed into a neutron, releasing a positron and a neutrino, which alters the atomic number of the element.

Positron Emission

Positron emission is a type of beta decay where a proton is converted into a neutron, resulting in the emission of a positron (the antimatter counterpart of an electron) and a neutrino. This process decreases the atomic number of the element by one while keeping the mass number unchanged. It is commonly observed in isotopes that are proton-rich and unstable.

Balanced Nuclear Equations

Balanced nuclear equations represent the transformation of one element into another during radioactive decay, ensuring that the total number of nucleons (protons and neutrons) and charge are conserved. In writing these equations, the initial and final isotopes, along with any emitted particles, must be accurately depicted to reflect the changes occurring in the nucleus during the decay process.

Recommended video:

Guided course

01:32

Balancing Chemical Equations

Related Practice

Textbook Question

Write balanced nuclear equations for the following transformations: (a) bismuth-213 undergoes alpha decay.

Textbook Question

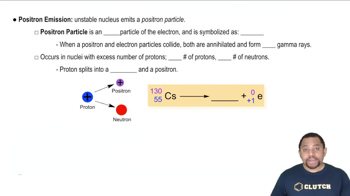
Write balanced nuclear equations for the following transformations:

(b) nitrogen-13 undergoes electron capture.

Textbook Question

Write balanced nuclear equations for the following transformations: (c) technicium-98 undergoes electron capture.

Textbook Question

Decay of which nucleus will lead to the following products: (a) bismuth-211 by beta decay?

Textbook Question

Decay of which nucleus will lead to the following products: (b) chromium-50 by positron emission?