Textbook Question
(c) What other substances are used as a moderator in nuclear reactor designs?
1
views
Ch.21 - Nuclear Chemistry
Chapter 21, Problem 63
A portion of the Sun’s energy comes from the reaction 4 11H → 42He + 2 0-1e, which requires a temperature of 106 to 107 K. Use the mass of the helium-4 nucleus given in Table 21.7 to determine how much energy is released per mol of hydrogen atoms.
Verified step by step guidance1
Step 1: Identify the nuclear reaction involved. The reaction is 4 protons (hydrogen nuclei) combining to form one helium-4 nucleus and two positrons.
Step 2: Determine the mass defect. Calculate the difference in mass between the reactants (4 hydrogen nuclei) and the products (1 helium-4 nucleus and 2 positrons). Use the given mass of the helium-4 nucleus and standard masses for protons and positrons.
Step 3: Convert the mass defect to energy. Use Einstein's equation, \( E = \Delta m c^2 \), where \( \Delta m \) is the mass defect and \( c \) is the speed of light, to find the energy released per reaction.
Step 4: Calculate the energy per mole. Since the reaction involves 4 hydrogen atoms, convert the energy per reaction to energy per mole by multiplying by Avogadro's number (\( 6.022 \times 10^{23} \) mol\(^{-1}\)).
Step 5: Summarize the result. The final step is to express the energy released per mole of hydrogen atoms in appropriate units, such as kilojoules per mole (kJ/mol).
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Nuclear Fusion
Nuclear fusion is the process by which two light atomic nuclei combine to form a heavier nucleus, releasing energy in the process. In the context of the Sun, hydrogen nuclei (protons) fuse to form helium, which is the primary source of the Sun's energy. This reaction occurs under extreme temperatures and pressures, allowing the strong nuclear force to overcome the electrostatic repulsion between positively charged protons.
Recommended video:
Guided course
02:06
Nuclear Binding Energy
Mass-Energy Equivalence
Mass-energy equivalence, encapsulated in Einstein's equation E=mc², states that mass can be converted into energy and vice versa. In nuclear reactions, a small amount of mass is lost when nuclei fuse, and this mass is converted into a significant amount of energy. Understanding this principle is crucial for calculating the energy released during fusion reactions, such as the one occurring in the Sun.
Recommended video:
Guided course
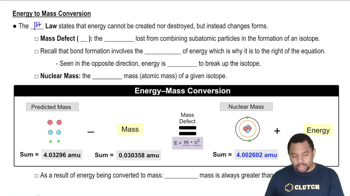
04:12Energy to Mass Conversion
Molar Mass and Energy Calculations
Molar mass is the mass of one mole of a substance, typically expressed in grams per mole. To determine the energy released per mole of hydrogen atoms in the fusion reaction, one must use the molar mass of the reactants and products, along with the energy released per reaction. This involves converting the mass defect (the difference in mass before and after the reaction) into energy using the mass-energy equivalence principle.
Recommended video:
Guided course
03:12Molar Mass Calculation Example
Related Practice
Textbook Question
Complete and balance the nuclear equations for the following fission or fusion reactions:
(a) 21H + 21H → 32He + _
(b) 23992U + 10n¡ → 13351Sb + 9841Nb + _ 10n
1
views
Textbook Question
Complete and balance the nuclear equations for the following fission reactions:
(a) 23592U + 10n → 16062Sm + 7230Zn + _ 10n
(b) 23994Pu + 10n → 14458Ce + _ + 2 10n
1
views
Textbook Question
The spent fuel elements from a fission reactor are much more intensely radioactive than the original fuel elements. (b) Given that only two or three neutrons are released per fission event and knowing that the nucleus undergoing fission has a neutron-to-proton ratio characteristic of a heavy nucleus, what sorts of decay would you expect to be dominant among the fission products?
1
views