Calculate the number of kilowatt-hours of electricity required to produce 1.0 * 103 kg (1 metric ton) of aluminum by electrolysis of Al3+ if the applied voltage is 4.50 V and the process is 45% efficient.

The Haber process is the principal industrial route for converting nitrogen into ammonia: N2(g) + 3 H2(g) → 2 NH3(g). (c) Calculate the standard emf of the Haber process at room temperature.
 Verified step by step guidance
Verified step by step guidanceKey Concepts
Haber Process
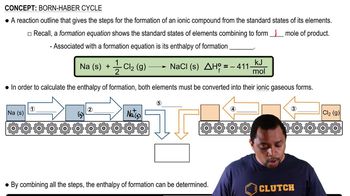
Standard Electromotive Force (emf)

Nernst Equation

The Haber process is the principal industrial route for converting nitrogen into ammonia: N2(g) + 3 H2(g) → 2 NH3(g) (b) Using the thermodynamic data in Appendix C, calculate the equilibrium constant for the process at room temperature.
Aqueous solutions of ammonia (NH3) and bleach (active ingredient NaOCl) are sold as cleaning fluids, but bottles of both of them warn: 'Never mix ammonia and bleach, as toxic gases may be produced.' One of the toxic gases that can be produced is chloroamine, NH2Cl. (a) What is the oxidation number of chlorine in bleach? (active ingredient NaOCl) are sold as cleaning fluids, but bottles of both of them warn: “Never mix ammonia and bleach, as toxic gases may be produced.” One of the toxic gases that can be produced is chloroamine, NH2Cl. (b) What is the oxidation number of chlorine in chloramine? (d) Another toxic gas that can be produced is nitrogen trichloride, NCl3. What is the oxidation number of N in nitrogen trichloride?
