(b) Using the mass of the proton from Table 2.1 and assuming its diameter is 1.0 * 10-15 m, calculate the density of a proton in g>cm3.

Verified step by step guidance

Identify the mass of a proton from Table 2.1, which is approximately 1.67 \times 10^{-27} \text{ kg}.

Convert the mass of the proton from kilograms to grams by using the conversion factor: 1 \text{ kg} = 1000 \text{ g}.

Assume the proton is spherical and use the formula for the volume of a sphere: V = \frac{4}{3} \pi r^3, where r is the radius of the proton.

Calculate the radius of the proton by dividing the given diameter (1.0 \times 10^{-15} \text{ m}) by 2.

Convert the volume from cubic meters to cubic centimeters using the conversion factor: 1 \text{ m}^3 = 10^6 \text{ cm}^3, and then calculate the density using the formula: \text{Density} = \frac{\text{mass}}{\text{volume}}.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Density

Density is defined as mass per unit volume, typically expressed in grams per cubic centimeter (g/cm³) in chemistry. It provides a measure of how much matter is contained in a given volume. To calculate density, one can use the formula: density = mass/volume. Understanding this concept is crucial for determining the density of a proton based on its mass and volume.

Mass of a Proton

The mass of a proton is a fundamental constant in physics and chemistry, approximately 1.67 x 10^-24 grams. This value is essential for calculations involving atomic and molecular masses. In the context of the question, knowing the mass of the proton allows for the calculation of its density when combined with its volume.

Volume of a Sphere

The volume of a sphere is calculated using the formula V = (4/3)πr³, where r is the radius. In this case, the diameter of the proton is given, so the radius can be determined by dividing the diameter by two. This volume is necessary to find the density of the proton, as it provides the space occupied by the mass of the proton.

Recommended video:

Guided course

02:35

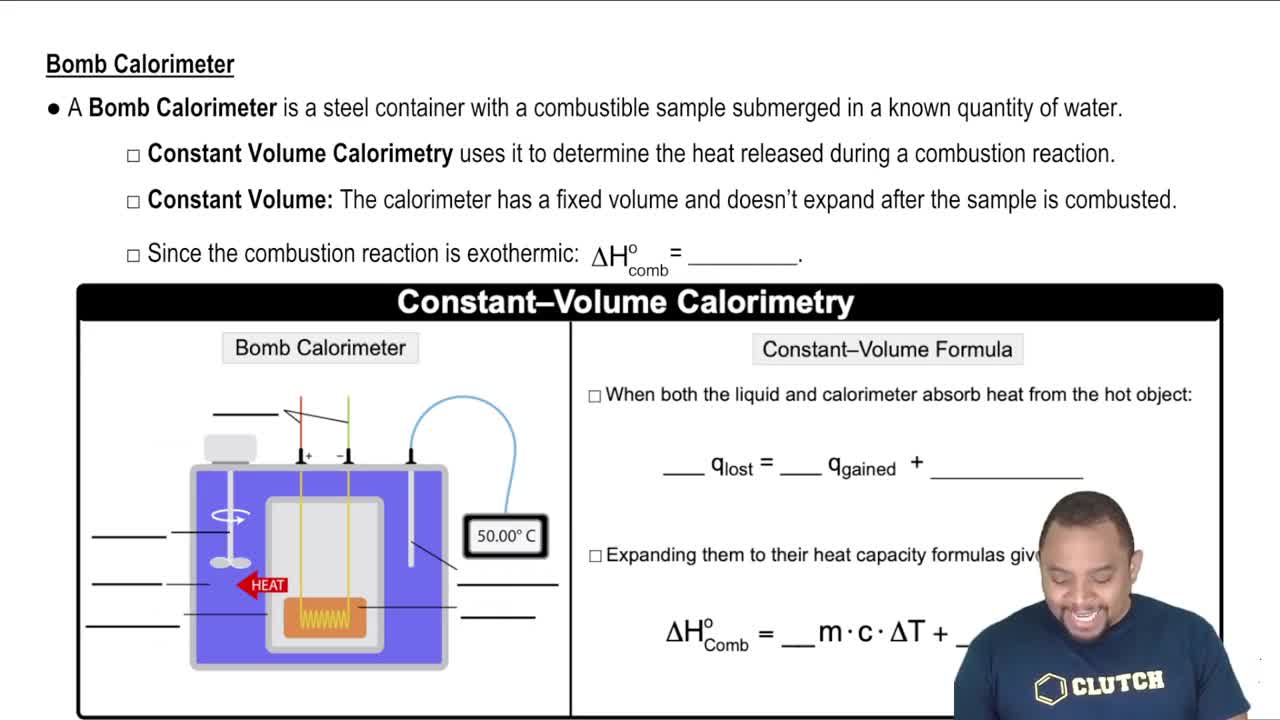
Constant-Volume Calorimetry

Related Practice

Textbook Question

"The diameter of a rubidium atom is 495 pm We will consider two different ways of placing the atoms on a surface. In arrangement A, all the atoms are lined up with one another to form a square grid. Arrangement B is called a close-packed arrangement because the atoms sit in the 'depressions' formed by the previous row of atoms:

Textbook Question

Very small semiconductor crystals, composed of approximately1000 to 10,000 atoms, are called quantum dots.Quantum dots made of the semiconductor CdSe are nowbeing used in electronic reader and tablet displays becausethey emit light efficiently and in multiple colors, dependingon dot size. The density of CdSe is 5.82 g/cm3.(b) CdSe quantum dots that are 2.5 nm in diameter emitblue light upon stimulation. Assuming that the dot is aperfect sphere and that the empty space in the dot canbe neglected, calculate how many Cd atoms are in onequantum dot of this size.

Textbook Question

(a) Assuming the dimensions of the nucleus and atom shown in Figure 2.10, what fraction of the volume of the atom is taken up by the nucleus?

views

Textbook Question

Identify the element represented by each of the following symbols and give the number of protons and neutrons in each: (a) ⁷⁴₃₃X

views

Textbook Question

Identify the element represented by each of the following symbols and give the number of protons and neutrons in each: (b) ¹²⁷₅₃X (c) ⁸⁶₃₆X (d) ⁶⁷₃₀X

views

Textbook Question

The nucleus of ⁶Li is a powerful absorber of neutrons. It exists in the naturally occurring metal to the extent of 7.5%. In the era of nuclear deterrence, large quantities of lithium were processed to remove 6Li for use in hydrogen bomb production. The lithium metal remaining after removal of ⁶Li was sold on the market. (a) What are the compositions of the nuclei of ⁶Li and ⁷Li?