Textbook Question
(c) In a particular spontaneous process, the number of microstates available to the system decreases. What can you conclude about the sign of ΔSsurr?

 Verified step by step guidance
Verified step by step guidance

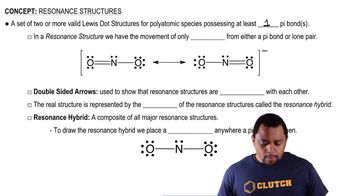
(c) In a particular spontaneous process, the number of microstates available to the system decreases. What can you conclude about the sign of ΔSsurr?
Would each of the following changes increase, decrease, or have no effect on the number of microstates available to a system: (b) decrease in volume
(a) In a chemical reaction, two gases combine to form a solid. What do you expect for the sign of ΔS?
(b) How does the entropy of the system change in the processes described in Exercise 19.12?