The value of K sp for Cd(OH) 2 is 2.5 × 10 -14 . (a) What is the molar solubility of Cd(OH) 2 ?

Identify the dissolution equation for Cd(OH) 2 : Cd(OH) 2 (s) ⇌ Cd 2+ (aq) + 2OH - (aq).. Write the expression for the solubility product constant (K sp ): K sp = [Cd 2+ ][OH - ] 2 .. Let the molar solubility of Cd(OH) 2 be 's'. Then, [Cd 2+ ] = s and [OH - ] = 2s.. Substitute the expressions for the ion concentrations into the K sp expression: K sp = (s)(2s) 2 = 4s 3 .. Set the K sp expression equal to the given K sp value and solve for 's': 4s 3 = 2.5 × 10 -14 .

The value of K sp for Cd(OH) 2 is 2.5 × 10 -14 . (a) What is the molar solubility of Cd(OH) 2 ?

hi everyone for this problem. It reads if the value of the solid ability product constant for lead to iodide is 9.8 times 10 to the negative nine what is its moller solly ability. So we want to calculate moller solly ability and the way that we're going to do this is we're going to solve for X. Or calculate for X. Which is going to give us the value for Moeller solly ability. And by calculate for X, we're going to create an ice table. Okay, so let's start off by writing out a balanced reaction. So our reaction balanced is going to be the following. And with this we can create an ice table. Remember that solids are ignored in the ice table. So we're just going to go ahead and ignore this. We have zero product. Okay, so that means our reaction is going to move in the forward direction and we're going to create product. So for our change, our initial is zero moller. For a change because we're creating product we're going to have a positive and we only have one mole. So this is going to be plus X. And this for the second product, our change is plus two X. So then we have X and two X. Now let's go ahead and write R K S. P expression, which is our solid ability product expression and this is going to equal and note that solids are ignored and concentrations is raised by the stoke E O metric coefficient. So are solid ability. Product constant is going to equal the concentration of products over the concentration of reactant. And when we do this, what this equates to is it's going to equal the concentration of products which we have our ions here raised to their coefficients. And because we don't include solids and the expression this is going to be all over one. So let's go ahead and write out. We know what the K. S. P. Expression or value is is 9.8 times 10 to the negative nine. So we have 9.8 times 10 to the negative nine, which is our key sp expression. This is this right here is going to equal now we're gonna plug in what's in the equilibrium row of our ice table for these two values here. Okay, so for the equilibrium row of our ice table, we have X times two X squared. Okay, so now what we're going to do is we're going to solve for X because when we solve for X, that's going to give us the solar cell ability. Okay, so let's go ahead and simplify this so that we can calculate for X. So when we simplify this, what we get is 9.8 times 10 to the negative nine is equal to. So this essentially is X times four X squared because we're foiling this out. Okay, so we have X times four X squared. So now the right side becomes four X cubed is equal to 9.8 times 10 to the negative nine. Okay, so let's divide both sides by four. And we're going to raise Yes. So we're going to divide both sides by four. And what we're going to get is X. is equal to 9.8 times 10 to the -9, divided by four, raise to one third so that we can get rid of the cube. Okay? So this is gonna all be raised to one third. So then what we get is X is equal to 1.3481 times 10 to the negative three. And so our final answer is 1. times 10 to the negative three molar. This is going to be the molar soluble itty. That is it for this problem. I hope this was helpful.

The value of Ksp for Cd(OH)2 is 2.5 × 10-14. (a) What is the molar solubility of Cd(OH)2?

Identify the dissolution equation for Cd(OH) 2 : Cd(OH) 2 (s) ⇌ Cd 2+ (aq) + 2OH - (aq). Write the expression for the solubility product constant (K sp ): K sp = [Cd 2+ ][OH - ] 2 . Let the molar solubility of Cd(OH) 2 be 's'. Then, [Cd 2+ ] = s and [OH - ] = 2s. Substitute the expressions for the ion concentrations into the K sp expression: K sp = (s)(2s) 2 = 4s 3 . Set the K sp expression equal to the given K sp value and solve for 's': 4s 3 = 2.5 × 10 -14 .

Ch.17 - Additional Aspects of Aqueous Equilibria

All textbooks

Brown 14th Edition

Ch.17 - Additional Aspects of Aqueous Equilibria

Problem 109a

Chapter 17, Problem 109a

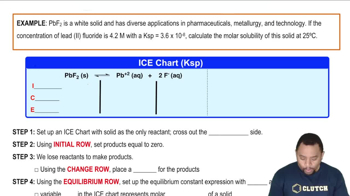
The value of K_sp for Cd(OH)₂ is 2.5 × 10^-14. (a) What is the molar solubility of Cd(OH)₂?

Verified step by step guidance

Identify the dissolution equation for Cd(OH)₂: Cd(OH)₂(s) ⇌ Cd²⁺(aq) + 2OH^-(aq).

Write the expression for the solubility product constant (K_sp): K_sp = [Cd²⁺][OH^-]².

Let the molar solubility of Cd(OH)₂ be 's'. Then, [Cd²⁺] = s and [OH^-] = 2s.

Substitute the expressions for the ion concentrations into the K_sp expression: K_sp = (s)(2s)² = 4s³.

Set the K_sp expression equal to the given K_sp value and solve for 's': 4s³ = 2.5 × 10^-14.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Solubility Product Constant (Ksp)

The solubility product constant (Ksp) is an equilibrium constant that applies to the solubility of sparingly soluble ionic compounds. It is defined as the product of the molar concentrations of the ions, each raised to the power of their coefficients in the balanced equation. For Cd(OH)2, Ksp = [Cd^2+][OH^-]^2, which helps determine how much of the compound can dissolve in water.

Molar Solubility

Molar solubility refers to the maximum concentration of a solute that can dissolve in a given volume of solvent at equilibrium. It is typically expressed in moles per liter (mol/L). In the case of Cd(OH)2, calculating the molar solubility involves determining the concentration of Cd^2+ and OH^- ions that can exist in solution when the compound is at its saturation point.

Stoichiometry of Dissolution

The stoichiometry of dissolution describes the ratio in which ions are produced when a compound dissolves. For Cd(OH)2, the dissolution can be represented as Cd(OH)2(s) ⇌ Cd^2+(aq) + 2OH^-(aq). This indicates that one mole of Cd(OH)2 produces one mole of Cd^2+ and two moles of OH^-, which is essential for relating Ksp to molar solubility.