Which, if any, of the following statements are true? (a) The stronger the base, the smaller the pKb. (b) The stronger the base, the larger the pKb. (c) The stronger the base, the smaller the Kb. (d) The stronger the base, the larger the Kb. (e) The stronger the base, the smaller the pKa of its conjugate acid. (f) The stronger the base, the larger the pKa of its conjugate acid.
Ch.16 - Acid-Base Equilibria

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 16, Problem 106
What is the pH of a solution that is 2.5 * 10^-9 M in NaOH? Does your answer make sense? What assumption do we normally make that is not valid in this case?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recognize that NaOH is a strong base and will dissociate completely in water to produce OH⁻ ions. Therefore, the concentration of OH⁻ ions in the solution is 2.5 \times 10^{-9} \text{ M}.
Step 2: Calculate the pOH of the solution using the formula \( \text{pOH} = -\log[\text{OH}^-] \). Substitute the concentration of OH⁻ ions into this formula.
Step 3: Use the relationship between pH and pOH, which is \( \text{pH} + \text{pOH} = 14 \), to find the pH of the solution.
Step 4: Consider the contribution of OH⁻ ions from the autoionization of water, which is significant in this case because the concentration of NaOH is very low. The concentration of OH⁻ from water is \( 1.0 \times 10^{-7} \text{ M} \).
Step 5: Recalculate the total OH⁻ concentration by adding the OH⁻ from NaOH and the OH⁻ from water. Use this total concentration to find the correct pOH and then the pH.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
pH Scale
The pH scale measures the acidity or basicity of a solution, ranging from 0 to 14. A pH of 7 is neutral, below 7 indicates acidity, and above 7 indicates basicity. The pH is calculated as the negative logarithm of the hydrogen ion concentration, pH = -log[H+]. In basic solutions, the concentration of hydroxide ions (OH-) is higher, which inversely affects the hydrogen ion concentration.
Recommended video:
Guided course
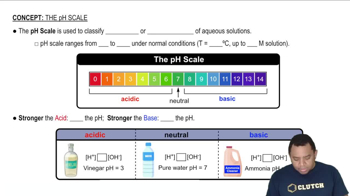
The pH Scale
Dissociation of Water
Water undergoes self-dissociation, producing equal concentrations of hydrogen ions (H+) and hydroxide ions (OH-). At 25°C, the concentration of H+ and OH- in pure water is 1.0 x 10^-7 M, leading to a neutral pH of 7. In very dilute solutions, such as the one in the question, the contribution of H+ from water becomes significant and must be considered when calculating pH.
Recommended video:
Guided course
Percent Dissociation Example
Assumption of Dilute Solutions
In dilute solutions, it is often assumed that the contribution of H+ ions from the solute is much greater than that from water. However, in this case, the concentration of NaOH is so low (2.5 x 10^-9 M) that the H+ concentration from water (1.0 x 10^-7 M) becomes comparable, invalidating the assumption. This necessitates a more careful calculation of pH, taking both contributions into account.
Recommended video:
Guided course
Solution Dilution Process
Related Practice
Textbook Question
Textbook Question
Predict how each molecule or ion would act, in the Brønsted-Lowry sense, in aqueous solution by writing 'acid,' 'base,' 'both,' or 'neither' on the line provided. (b) Prozac
Textbook Question
Calculate the pH of a solution made by adding 2.50 g of lithium oxide 1Li2O2 to enough water to make 1.500 L of solution.
Textbook Question
Butyric acid is responsible for the foul smell of rancid butter. The pKa of butyric acid is 4.84. (a) Calculate the pKb for the butyrate ion.
