The following equilibria were measured at 823 K: CoO(s) + H2(g) ⇄ Co(s) + H2O(g) Kc = 67; H2(g) + CO2(g) ⇄ CO(g) + H2O(g) Kc = 0.14. (c) If you were to place 5.00 g of CoO(s) in a sealed tube with a volume of 250 mL that contains CO(g) at a pressure of 1.00 atm and a temperature of 298 K, what is the concentration of the CO gas? Assume there is no reaction at this temperature and that the CO behaves as an ideal gas (you can neglect the volume of the solid).

Verified step by step guidance

Step 1: Begin by identifying the relevant information given in the problem. You have 5.00 g of CoO(s) in a sealed tube with a volume of 250 mL, containing CO(g) at a pressure of 1.00 atm and a temperature of 298 K. The problem states that there is no reaction at this temperature, and CO behaves as an ideal gas.

Step 2: Use the ideal gas law to find the concentration of CO gas. The ideal gas law is given by the equation:

P = \frac{n R T}{V}

, where P is the pressure, n is the number of moles, R is the ideal gas constant, T is the temperature, and V is the volume.

Step 3: Rearrange the ideal gas law to solve for the concentration of CO gas, which is the number of moles per unit volume:

\frac{n}{V} = \frac{P}{R T}

. This expression gives the concentration in moles per liter.

Step 4: Substitute the known values into the rearranged equation. Use P = 1.00 atm, R = 0.0821 L atm/mol K (ideal gas constant), T = 298 K, and V = 0.250 L (converted from 250 mL).

Step 5: Calculate the concentration of CO gas using the substituted values. This will give you the concentration in moles per liter, which is the desired quantity.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Equilibrium Constant (Kc)

The equilibrium constant (Kc) is a numerical value that expresses the ratio of the concentrations of products to reactants at equilibrium for a given reaction at a specific temperature. It provides insight into the extent of a reaction; a large Kc indicates that products are favored, while a small Kc suggests reactants are favored. Understanding Kc is crucial for predicting the direction of a reaction and the concentrations of species at equilibrium.

Ideal Gas Law

The Ideal Gas Law is a fundamental equation in chemistry that relates the pressure, volume, temperature, and number of moles of an ideal gas. It is expressed as PV = nRT, where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is temperature in Kelvin. This law allows for the calculation of gas concentrations and behaviors under various conditions, assuming the gas behaves ideally.

Concentration Calculation

Concentration is defined as the amount of a substance (solute) present in a given volume of solution. It is typically expressed in moles per liter (Molarity, M). To calculate the concentration of a gas in a sealed container, one can use the Ideal Gas Law to determine the number of moles of gas present and then divide by the volume of the container. This concept is essential for understanding how gas quantities relate to their physical conditions.

Recommended video:

Guided course

07:35

Calculate Concentration of the Basic Form

Related Practice

Textbook Question

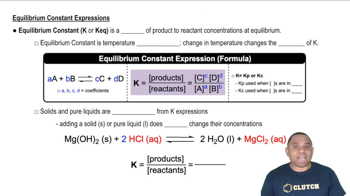
Consider the hypothetical reaction A(𝑔) + 2 B(𝑔) ⇌ 2 C(𝑔), for which 𝐾_𝑐= 0.25 at a certain temperature. A 1.00-L reaction vessel is loaded with 1.00 mol of compound C, which is allowed to reach equilibrium. Let the variable x represent the number of mol/L of compound A present at equilibrium.

(d) The equation from part (c) is a cubic equation (one that has the form ax3 + bx2 + cx + d = 0). In general, cubic equations cannot be solved in closed form. However, you can estimate the solution by plotting the cubic equation in the allowed range of x that you specified in part (b). The point at which the cubic equation crosses the x-axis is the solution.

(e) From the plot in part (d), estimate the equilibrium concentrations of A, B, and C. (Hint: You can check the accuracy of your answer by substituting these concentrations into the equilibrium expression.)

views

Textbook Question

At a temperature of 700 K, the forward and reverse rate constants for the reaction 2 HI(g) ⇌ H₂(g) + I₂(g) are k_f = 1.8×10⁻³⁰ M⁻¹s⁻¹ and k_r = 0.063 M⁻¹s⁻¹.

(a) What is the value of the equilibrium constant K_c at 700 K?

(b) Is the forward reaction endothermic or exothermic if the rate constants for the same reaction have values of k_f= 0.097M⁻¹s⁻¹ and k_r= 2.6 M⁻¹s⁻¹ at 800 K?

Textbook Question

The following equilibria were measured at 823 K: CoO(s) + H₂(g) ⇌ Co(s) + H₂O(g) K_c = 67 H₂(g) + CO₂(g) ⇌ CO(g) + H₂O(g) Kc = 0.14 (a) Use these equilibria to calculate the equilibrium constant, K_c, for the reaction CoO(s) + CO(g) ⇌ Co(s) + CO₂(g) at 823 K.

Textbook Question

The following equilibria were measured at 823 K: CoO(s) + H₂(g) ⇌ Co(s) + H₂O(g) K_c = 67 H₂(g) + CO₂(g) ⇌ CO(g) + H₂O(g) Kc = 0.14 (d) If the reaction vessel from part (c) is heated to 823 K and allowed to come to equilibrium, how much CoO(s) remains?

views

Textbook Question

The phase diagram for SO₂ is shown here. (d) At which of the three points marked in red does SO₂(g) most closely approach ideal-gas behavior?