Skip to main content
Pearson+ LogoPearson+ Logo
Ch.15 - Chemical Equilibrium
All textbooksBrown 14th EditionCh.15 - Chemical EquilibriumProblem 78
Chapter 15, Problem 78

As shown in Table 15.2, the equilibrium constant for the reaction N2(g) + 3 H2(g) ⇌ 2 NH3(g) is Kp = 4.34 * 10^-3 at 300 _x001F_C. Pure NH3 is placed in a 1.00-L flask and allowed to reach equilibrium at this temperature. There are 1.05 g NH3 in the equilibrium mixture. (a) What are the masses of N2 and H2 in the equilibrium mixture? (b) What is the total pressure in the vessel?

Verified step by step guidance
1
Convert the mass of NH3 at equilibrium to moles using its molar mass. The molar mass of NH3 is approximately 17.03 g/mol. Use the formula: \( \text{moles of NH}_3 = \frac{\text{mass of NH}_3}{\text{molar mass of NH}_3} \).
Set up an ICE (Initial, Change, Equilibrium) table for the reaction N2(g) + 3 H2(g) ⇌ 2 NH3(g). Assume initial moles of N2 and H2 are zero, and calculate the change in moles of NH3 as it dissociates to reach equilibrium.
Use the equilibrium constant expression for Kp: \( K_p = \frac{(P_{\text{NH}_3})^2}{(P_{\text{N}_2})(P_{\text{H}_2})^3} \). Express the partial pressures in terms of the change in moles and the total volume of the flask.
Solve the equilibrium expression for the change in moles of N2 and H2. Use the stoichiometry of the reaction to relate the change in moles of NH3 to the changes in moles of N2 and H2.
Calculate the total pressure in the vessel using the ideal gas law: \( P = \frac{nRT}{V} \), where n is the total moles of gas at equilibrium, R is the ideal gas constant, T is the temperature in Kelvin, and V is the volume of the flask.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Equilibrium Constant (Kp)

The equilibrium constant (Kp) quantifies the ratio of the concentrations of products to reactants at equilibrium for a given reaction at a specific temperature. For the reaction N2(g) + 3 H2(g) ⇌ 2 NH3(g), Kp = 4.34 * 10^-3 indicates that at equilibrium, the concentration of NH3 is relatively low compared to N2 and H2. Understanding Kp is essential for calculating the amounts of reactants and products in equilibrium mixtures.
Recommended video:
Guided course
03:20
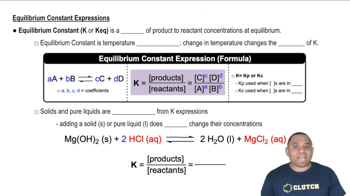
Equilibrium Constant Expressions

Stoichiometry

Stoichiometry involves the calculation of reactants and products in chemical reactions based on their molar ratios as defined by the balanced equation. In this case, the stoichiometric coefficients from the reaction indicate that 1 mole of N2 reacts with 3 moles of H2 to produce 2 moles of NH3. This concept is crucial for determining the masses of N2 and H2 present in the equilibrium mixture based on the amount of NH3.
Recommended video:
Guided course
01:16
Stoichiometry Concept

Ideal Gas Law

The Ideal Gas Law (PV = nRT) relates the pressure, volume, temperature, and number of moles of a gas. In this scenario, it can be used to calculate the total pressure in the vessel once the moles of N2 and H2 are determined. Understanding this law is vital for solving part (b) of the question, as it allows for the conversion of moles to pressure in a given volume at a specific temperature.
Recommended video:
Guided course
01:15
Ideal Gas Law Formula
Related Practice
Textbook Question

Consider the hypothetical reaction A(g) ⇌ 2 B(g). A flask is charged with 0.75 atm of pure A, after which it is allowed to reach equilibrium at 0°C. At equilibrium, the partial pressure of A is 0.36 atm. (c) What could we do to maximize the yield of B?

Textbook Question

As shown in Table 15.2, the equilibrium constant for the reaction N2(g) + 3 H2(g) ⇌ 2 NH3(g) is Kp = 4.34 × 10-3 at 300°C. Pure NH3 is placed in a 1.00-L flask and allowed to reach equilibrium at this temperature. There are 1.05 g NH3 in the equilibrium mixture. (b) What was the initial mass of ammonia placed in the vessel?

1
views
Textbook Question

For the equilibrium PH3BCl3(𝑠) ⇌ PH3(𝑔) + BCl3(𝑔) 𝐾𝑝 = 0.052 at 60 °C. (b) After 3.00 g of solid PH3BCl3 is added to a closed 1.500-L vessel at 60 °C, the vessel is charged with 0.0500 g of BCl3(𝑔). What is the equilibrium concentration of PH3?

2
views