Skip to main content
Pearson+ LogoPearson+ Logo
Ch.11 - Liquids and Intermolecular Forces
All textbooksBrown 14th EditionCh.11 - Liquids and Intermolecular ForcesProblem 96
Chapter 11, Problem 96

The vapor pressure of a volatile liquid can be determined by slowly bubbling a known volume of gas through it at a known temperature and pressure. In an experiment, 5.00 L of N2 gas is passed through 7.2146 g of liquid benzene (C6H6) at 26.0 °C. The liquid remaining after the experiment weighs 5.1493 g. Assuming that the gas becomes saturated with benzene vapor and that the total gas volume and temperature remain constant, what is the vapor pressure of the benzene in torr?

Verified step by step guidance
1
Calculate the mass of benzene that has evaporated by subtracting the final mass of the liquid from the initial mass: \( \text{mass evaporated} = 7.2146 \text{ g} - 5.1493 \text{ g} \).
Convert the mass of evaporated benzene to moles using its molar mass: \( \text{moles of C}_6\text{H}_6 = \frac{\text{mass evaporated}}{\text{molar mass of C}_6\text{H}_6} \).
Use the ideal gas law to find the partial pressure of benzene vapor. First, calculate the total moles of gas (N2 + benzene vapor) using the ideal gas law: \( PV = nRT \).
Determine the moles of N2 gas using the ideal gas law, assuming the initial conditions (before benzene evaporation) and subtract the moles of benzene vapor to find the moles of N2.
Calculate the vapor pressure of benzene by using the ratio of moles of benzene vapor to total moles of gas and multiplying by the total pressure: \( P_{\text{benzene}} = \left( \frac{\text{moles of C}_6\text{H}_6}{\text{total moles}} \right) \times P_{\text{total}} \).

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Vapor Pressure

Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid phase at a given temperature. It reflects the tendency of molecules to escape from the liquid phase into the vapor phase. The higher the vapor pressure, the more volatile the substance, indicating that it evaporates easily. Understanding vapor pressure is crucial for determining how much of a liquid will evaporate under specific conditions.
Recommended video:
Guided course
02:40
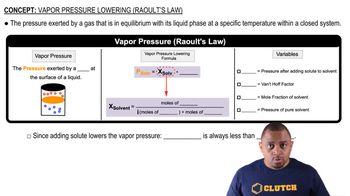
Raoult's Law and Vapor Pressure

Ideal Gas Law

The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law is essential for calculating the behavior of gases under varying conditions. In this experiment, it helps to understand how the volume of nitrogen gas and the temperature affect the saturation of benzene vapor in the gas phase, allowing for the determination of vapor pressure.
Recommended video:
Guided course
01:15
Ideal Gas Law Formula

Mass Loss and Molar Mass

In this experiment, the mass loss of benzene is critical for calculating the amount of benzene that evaporated. By knowing the initial and final masses of the liquid, one can determine the mass of benzene that transitioned to vapor. Additionally, the molar mass of benzene (approximately 78.11 g/mol) is necessary to convert the mass of evaporated benzene into moles, which can then be used to find the vapor pressure using the Ideal Gas Law.
Recommended video:
Guided course
02:11
Molar Mass Concept
Related Practice
Textbook Question

The vapor pressure of ethanol (C2H5OH) at 19 °C is 40.0 torr. A 1.00-g sample of ethanol is placed in a 2.00 L container at 19 °C. If the container is closed and the ethanol is allowed to reach equilibrium with its vapor, how many grams of liquid ethanol remain?

Textbook Question
Liquid butane (C4H10) is stored in cylinders to be used as a fuel. The normal boiling point of butane is listed as -0.5 °C. (b) Suppose the valve to the tank is opened and a few liters of butane are allowed to escape rapidly. What do you expect would happen to the temperature of the remaining liquid butane in the tank? Explain.
Textbook Question

Using information in Appendices B and C, calculate the minimum grams of propane, C3H8(g), that must be combusted to provide the energy necessary to convert 5.50 kg of ice at -20 °C to liquid water at 75 °C

Textbook Question

The relative humidity of air equals the ratio of the par- tial pressure of water in the air to the equilibrium vapor pressure of water at the same temperature times 100%. If the relative humidity of the air is 58% and its temperature is 68 °F, how many molecules of water are present in a room measuring12ft * 10ft * 8ft?