A 30.0-cm-long cylindrical plastic tube, sealed at one end, is filled with acetic acid. The mass of acetic acid needed to fill the tube is found to be 89.24 g. The density of acetic acid is 1.05 g/mL. Calculate the inner diameter of the tube in centimeters.

Verified step by step guidance

Calculate the volume of acetic acid using its mass and density. Use the formula: \( \text{Volume} = \frac{\text{Mass}}{\text{Density}} \).

Convert the volume from milliliters to cubic centimeters, knowing that 1 mL = 1 cm³.

Recognize that the volume of a cylinder is given by the formula: \( V = \pi r^2 h \), where \( r \) is the radius and \( h \) is the height of the cylinder.

Rearrange the formula to solve for the radius: \( r = \sqrt{\frac{V}{\pi h}} \).

Double the radius to find the diameter of the tube, since \( \text{Diameter} = 2r \).

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Density

Density is defined as mass per unit volume and is a crucial property of substances. In this case, the density of acetic acid (1.05 g/mL) allows us to relate the mass of the acetic acid (89.24 g) to its volume. By using the formula density = mass/volume, we can rearrange it to find the volume of acetic acid in the tube, which is essential for further calculations.

Volume of a Cylinder

The volume of a cylinder can be calculated using the formula V = πr²h, where r is the radius and h is the height (or length) of the cylinder. In this problem, the height is given as 30.0 cm. Knowing the volume of acetic acid from the previous step allows us to solve for the radius, which is necessary to find the inner diameter of the tube.

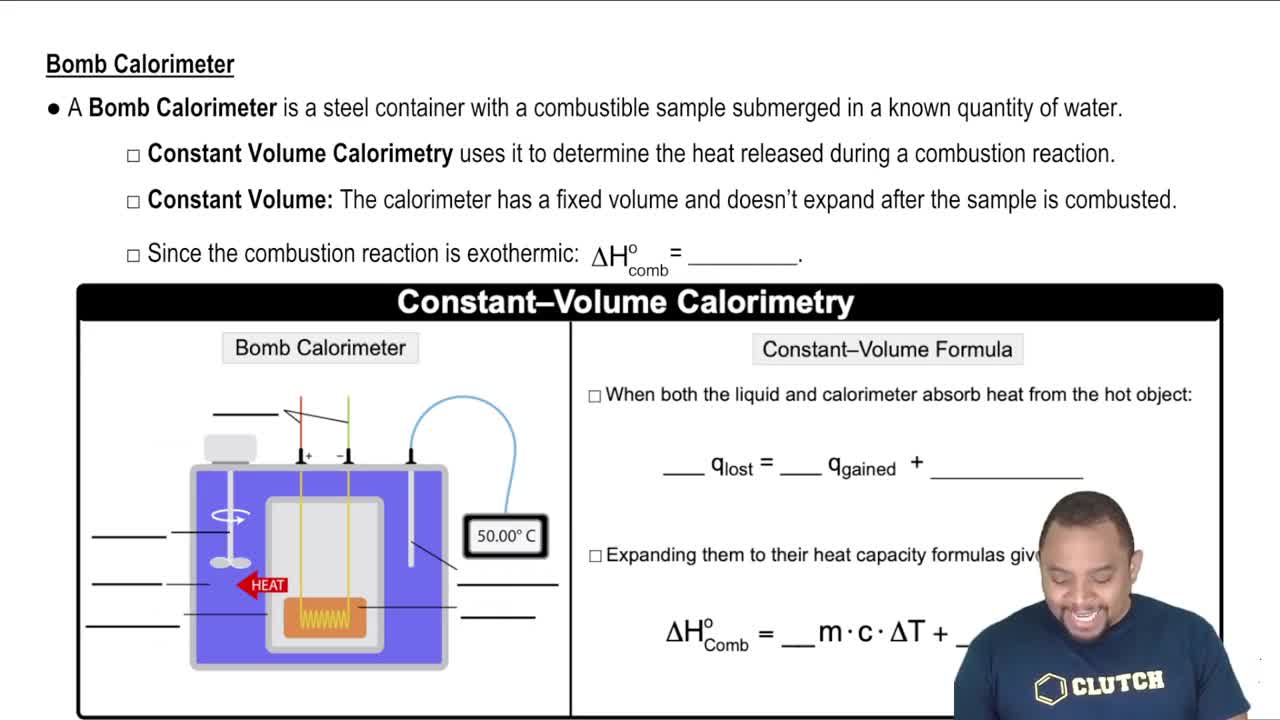
Diameter Calculation

The diameter of a cylinder is twice the radius (d = 2r). Once we have calculated the radius from the volume of acetic acid, we can easily find the diameter. This step is essential for providing the final answer to the question regarding the inner diameter of the tube.

Recommended video:

Guided course

02:28

Stoichiometric Rate Calculations

Related Practice

Textbook Question

The total rate at which power is used by humans worldwideis approximately 15 TW (terawatts). The solar flux averagedover the sunlit half of Earth is 680 W>m2 (assumingno clouds). The area of Earth's disc as seen from the Sun is1.28 * 1014 m2. The surface area of Earth is approximately197,000,000 square miles. How much of Earth's surfacewould we need to cover with solar energy collectors to powerthe planet for use by all humans? Assume that the solar energycollectors can convert only 10% of the available sunlightinto useful power

views

Textbook Question

Gold is alloyed (mixed) with other metals to increase its hardness in making jewelry. (a) Consider a piece of gold jewelry that weighs 9.85 g and has a volume of 0.675 cm3. The jewelry contains only gold and silver, which have densities of 19.3 and 10.5 g/cm³, respectively. If the total volume of the jewelry is the sum of the volumes of the gold and silver that it contains, calculate the percentage of gold (by mass) in the jewelry. (b) The relative amount of gold in an alloy is commonly expressed in units of carats. Pure gold is 24 carat, and the percentage of gold in an alloy is given as a percentage of this value. For example, an alloy that is 50% gold is 12 carat. State the purity of the gold jewelry in carats.

Textbook Question

Judge the following statements as true or false. If you believe a statement to be false, provide a corrected version. (a) Air and water are both elements.

views