The steps below show three of the steps in the radioactive decay chain for 23290Th. The half-life of each isotope is shown below the symbol of the isotope. (d) The next step in the decay chain is an alpha emission. What is the next isotope in the chain? [Sections 21.2 and 21.4]
Ch.21 - Nuclear Chemistry

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 21, Problem 6b
The accompanying graph illustrates the decay of 8842Mo, which decays via positron emission. (b) What is the rate constant for the decay? [Section 21.4]
 Verified step by step guidance
Verified step by step guidance1
Identify the type of decay process: The problem states that 8842Mo decays via positron emission. This is a type of radioactive decay where a proton is converted into a neutron, releasing a positron and a neutrino.
Understand the relationship between half-life and the rate constant: The rate constant (k) for a first-order decay process can be determined using the relationship between the half-life (t1/2) and the rate constant, given by the formula: t1/2 = \( \frac{0.693}{k} \).
Determine the half-life from the graph: Analyze the graph provided to find the time it takes for the amount of 8842Mo to decrease to half of its initial value. This time is the half-life (t1/2).
Use the half-life to calculate the rate constant: Once the half-life is known, rearrange the formula to solve for the rate constant: k = \( \frac{0.693}{t1/2} \).
Substitute the half-life value into the equation: Insert the half-life value obtained from the graph into the equation to find the rate constant k.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radioactive Decay
Radioactive decay is the process by which unstable atomic nuclei lose energy by emitting radiation. This can occur through various modes, including alpha decay, beta decay, and positron emission. In the case of the isotope 88Mo, positron emission involves the conversion of a proton into a neutron, resulting in the emission of a positron and a neutrino.
Recommended video:
Guided course

Rate of Radioactive Decay
Rate Constant
The rate constant (k) is a proportionality factor in the equation that describes the rate of a chemical reaction or decay process. For radioactive decay, it is related to the half-life of the substance and indicates how quickly the substance will decay. The relationship is given by the equation k = ln(2) / t1/2, where t1/2 is the half-life.
Recommended video:
Guided course
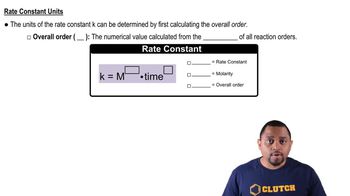
Rate Constant Units
Exponential Decay
Exponential decay describes the process by which the quantity of a radioactive substance decreases over time at a rate proportional to its current value. This can be mathematically represented by the equation N(t) = N0 e^(-kt), where N(t) is the quantity at time t, N0 is the initial quantity, and k is the rate constant. Understanding this concept is crucial for calculating the rate constant from decay data.
Recommended video:
Guided course
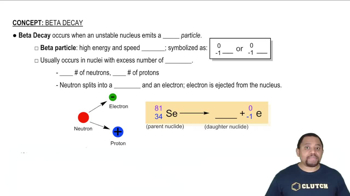
Beta Decay
Related Practice
Textbook Question
2
views
Textbook Question
The accompanying graph illustrates the decay of 8842Mo, which decays via positron emission. (a) What is the halflife of the decay? [Section 21.4]
1
views
Textbook Question
The accompanying graph illustrates the decay of 8842Mo, which decays via positron emission. (c) What fraction of the original sample of 8842Mo remains after 12 min? [Section 21.4]
1
views
Textbook Question
The accompanying graph illustrates the decay of 8842Mo, which decays via positron emission. (d) What is the product of the decay process? [Section 21.4]
1
views
