Americium-241 is used in smoke detectors. It has a first-order rate constant for radioactive decay of k = 1.6 * 10-3 yr-1. By contrast, iodine-125, which is used to test for thyroid functioning, has a rate constant for radioactive decay of k = 0.011 day-1. (c) How much of a 1.00-mg sample of each isotope remains after three half-lives? (d) How much of a 1.00-mg sample of each isotope remains after 4 days?
Ch.14 - Chemical Kinetics

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 14, Problem 101c
The rate of a first-order reaction is followed by spectroscopy, monitoring the absorbance of a colored reactant at 520 nm. The reaction occurs in a 1.00-cm sample cell, and the only colored species in the reaction has an extinction coefficient of 5.60 × 103 M-1 cm-1 at 520 nm.
(c) Calculate the half-life of the reaction.
 Verified step by step guidance
Verified step by step guidance1
First, we need to understand that the rate constant (k) of a first-order reaction is related to the half-life (t1/2) by the equation: t1/2 = 0.693 / k.
Next, we know that the absorbance (A) of a solution is given by the Beer-Lambert law: A = εlc, where ε is the molar absorptivity (or extinction coefficient), l is the path length, and c is the concentration. In this case, we are given ε and l, but not c or A.
However, we know that for a first-order reaction, the concentration of the reactant decreases exponentially with time, and this decrease is reflected in the absorbance. Therefore, we can write: A = A0e^-kt, where A0 is the initial absorbance, k is the rate constant, and t is the time.
By rearranging this equation, we can solve for k: k = -ln(A/A0) / t. Note that this equation gives the rate constant in terms of the ratio of the final to initial absorbance, which is a dimensionless quantity, and the time, which must be in the same units as the half-life.
Finally, we can substitute this expression for k into the equation for the half-life to find: t1/2 = 0.693 / (-ln(A/A0) / t). This equation allows us to calculate the half-life of the reaction in terms of the initial and final absorbance and the time.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
First-Order Reactions
First-order reactions are chemical reactions where the rate is directly proportional to the concentration of one reactant. This means that as the concentration of the reactant decreases, the rate of the reaction also decreases. The mathematical representation of a first-order reaction is given by the equation: rate = k[A], where k is the rate constant and [A] is the concentration of the reactant.
Recommended video:
Guided course

First-Order Reactions
Absorbance and Beer-Lambert Law
The Beer-Lambert Law relates the absorbance of light to the properties of the material through which the light is traveling. It states that absorbance (A) is equal to the product of the extinction coefficient (ε), the concentration (c) of the absorbing species, and the path length (l) of the sample: A = εcl. This law is crucial for determining the concentration of reactants in a solution based on their absorbance at a specific wavelength.
Recommended video:
Guided course

Gay Lussac's Law
Half-Life of a Reaction
The half-life of a reaction is the time required for the concentration of a reactant to decrease to half of its initial value. For first-order reactions, the half-life is constant and can be calculated using the formula: t1/2 = 0.693/k, where k is the rate constant. This concept is essential for understanding the kinetics of the reaction and predicting how long it will take for the reactant concentration to diminish.
Recommended video:
Guided course
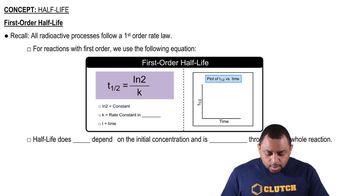
First-Order Half-Life
Related Practice
Textbook Question
Textbook Question
The rate of a first-order reaction is followed by spectroscopy, monitoring the absorbance of a colored reactant at 520 nm. The reaction occurs in a 1.00-cm sample cell, and the only colored species in the reaction has an extinction coefficient of 5.60 × 103 M-1 cm-1 at 520 nm.
(a) Calculate the initial concentration of the colored reactant if the absorbance is 0.605 at the beginning of the reaction.
Textbook Question
The rate of a first-order reaction is followed by spectroscopy, monitoring the absorbance of a colored reactant at 520 nm. The reaction occurs in a 1.00-cm sample cell, and the only colored species in the reaction has an extinction coefficient of 5.60 × 103 M-1 cm-1 at 520 nm.
(d) How long does it take for the absorbance to fall to 0.100?
