Table of contents
- 0. Functions(0)
- Introduction to Functions(0)
- Piecewise Functions(0)
- Properties of Functions(0)
- Common Functions(0)
- Transformations(0)
- Combining Functions(0)
- Exponent rules(0)
- Exponential Functions(0)
- Logarithmic Functions(0)
- Properties of Logarithms(0)
- Exponential & Logarithmic Equations(0)
- Introduction to Trigonometric Functions(0)
- Graphs of Trigonometric Functions(0)
- Trigonometric Identities(0)
- Inverse Trigonometric Functions(0)
- 1. Limits and Continuity(0)
- 2. Intro to Derivatives(0)
- 3. Techniques of Differentiation(0)
- 4. Applications of Derivatives(0)
- 5. Graphical Applications of Derivatives(0)
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions(0)
- 7. Antiderivatives & Indefinite Integrals(0)
- 8. Definite Integrals(0)
- 9. Graphical Applications of Integrals(0)
- 10. Physics Applications of Integrals (0)
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions(0)
- 12. Techniques of Integration(0)
- 13. Intro to Differential Equations(0)
- 14. Sequences & Series(0)
- 15. Power Series(0)
- 16. Parametric Equations & Polar Coordinates(0)
5. Graphical Applications of Derivatives
Applied Optimization
5. Graphical Applications of Derivatives
Applied Optimization: Videos & Practice Problems
9 of 0
Problem 9Multiple Choice
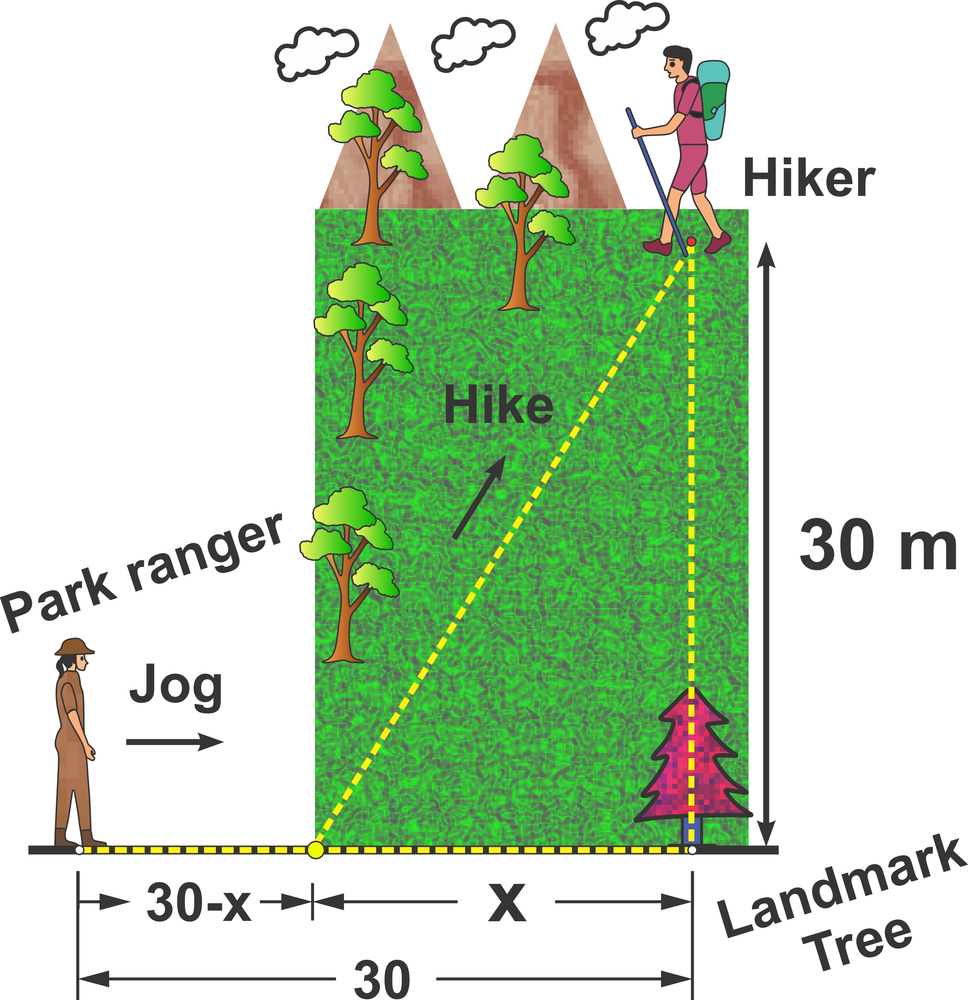
A park ranger needs to quickly get from their current location to a lost hiker who is 30 m away from a landmark tree, which is 30 m directly east of the ranger. The ranger can jog at a speed of 6 m/s on the trail and hike through the woods at a speed of 2 m/s. Determine the travel time function T(x), where .
0 Comments
