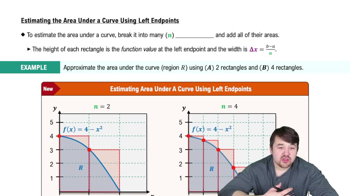
Rectangles beneath a line
a. A rectangle is constructed with one side on the positive x-axis, one side on the positive y-axis, and the vertex opposite the origin on the line y = 10 - 2x. What dimensions maximize the area of the rectangle? What is the maximum area?