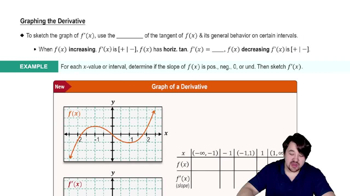
{Use of Tech} Bungee jumper A woman attached to a bungee cord jumps from a bridge that is 30 m above a river. Her height in meters above the river t seconds after the jump is y(t) = 15(1+e^−t cos t), for t ≥ 0.
b. Use a graphing utility to determine when she is moving downward and when she is moving upward during the first 10 s.